| The Slitting Method for Residual Stress Measurement: : Theory |
The Basic Theory For Incremental Slitting Measurements of Residual Stress:
Prime, M. B., and Hill, M. R., 2006, "Uncertainty, Model Error, and Order Selection for Series-Expanded, Residual-Stress Inverse Solutions," Journal of Engineering Materials and Technology, 128(2), pp. 175-185. preprint (pdf). (LA-UR-05-2597).
PULSE METHOD: For an alternative way of solving the inverse problem, this time using Tikhonov regularization, see: Schajer, G. S., and Prime, M. B., 2006, "Use of Inverse Solutions for Residual Stress Measurements," Journal of Engineering Materials and Technology, 128(3), 375-382. preprint (pdf). (LA-UR-04-5890) This approach is superior for rapidly varying stresses that cannot be fit with a series of continuous polynomials. Referred to as "pulse" method.
Experimental
First make a cut of progressively increasing depth. Measure strain at each depth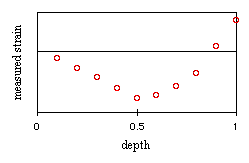
Analytical
Assume that you can write the still unknown residual stresses as a series expansion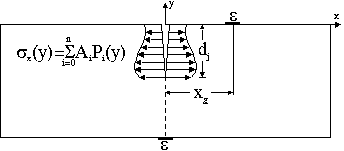
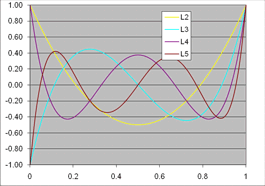
Now our unknowns are just the coefficients A. The P's can be a power series, Legendre polynomials, Fourier series, etc. Legendre polynomials are shown below.
unknown residual stresses as series expansion
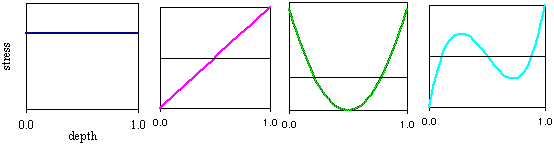
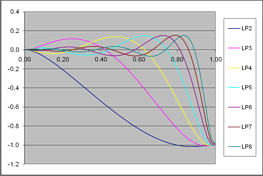
For each P we need to know the strain as a function of slot depth that would be measured for such a stress. This is the Compliance function, C. Actual compliance functions for the above stress functions are shown below.
Corresponding Strains - Compliance functions
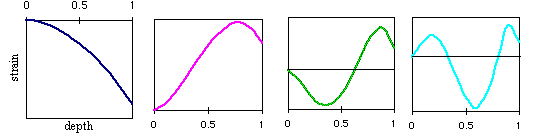
(These are notional compliance functions for a top gage near the cut, others will look different) See the discussion below for information on how these compliance functions
are calculated.
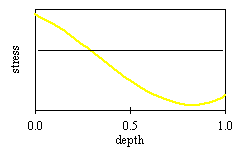
| What do compliance functions for through-thickness measurements really look like? | |
For Legenre polynomials like this through the thickness. Thickness is normalized by the full thickness. |
The Compliances for a gage opposite the cut (back face) look like this.This is for E = 1 and Poisson's ratio = 0 and can be sclaed for opther elastic properties. |
Numerical
Now find the linear combination of the above compliance functions that best fits the measured strains. Such a least squares fit can be written in matrix form as: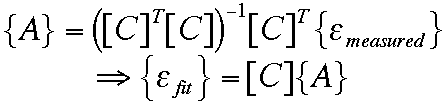
This gives the A's, hence the residual stresses:
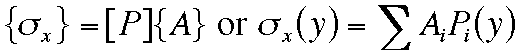
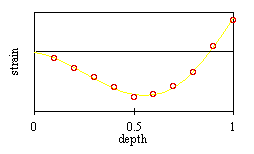
The signs are correct in this example. A positive residual stress will produce negative strain readings on the surface near the slot.
Discussion
This method of reducing the data and solving for stresses is very powerful. The use of a least squares fit means that the stress prediction results from a best fit curve of the experimental strain data. Because the curve does not have to pass exactly through all of the data points, it is very tolerant of small measurement errors. This technique was originally developed for the Hole Drilling method as the "Power Series" method of solving for residual stress [Schajer, G.S., "Application of Finite Element Calculations to Residual Stress Measurements," J. of Engineering Materials and Technology, V. 103, 1981, pp. 157-163.] However the character of the strains measured by hole drilling limit its applicability. For the compliance method,it works great - see the ring test. For more theoretical details and an extension to rapidly varying residual stress fields (ref #23) see the references.Some researchers distrust this least squares fit and insist on reducing the data at each increment. If you try some test data and add in some noise, you'll find that using a step by step inversion greatly increases the error.
Calculating Compliances
To apply this method, one must calculate the compliance functions. It was originally done using fracture mechanics solutions - see the references section, refs 1,2,4,8,9,10 and 26 for examples. They can also be calculated using finite elements or other numerical techniques. Of course, experimentally one introduces finite width slots rather than cracks. The body force method has been used to calculate compliances for finite width slots simply and accurately - see the references section, refs 20 & 27, for examples.