| The Slitting Method for Residual Stress Measurement: : Resources and Help |
Resources and Help
Because it requires the solution of an elastic inverse problem, data reduction for slitting measurements takes some effort to learn and some practice to get good at. This page offers some help.
Experimental Procedure
Some help with besat experimental practices is:
M. B. Prime, “Experimental Procedure for Crack Compliance (Slitting) Measurements of Residual Stress,” LA-UR-03-8629, Los Alamos National Laboratory Report, 2003.
Free Data Reduction (or go to Data Reduction Yourself)
If you have simple data you have taken for research purposes, I am willing to reduce the data and provide you stress results and uncertainty estimates. This offer only applies to strain data from a back gauge on a simple beam, bar, plate, or circular disk geometry. Please do your best to perform the test and post-test measurements and corrections as described in the experimental procedure report (LA-UR-03-8629). Please fill out this spreadsheet with your data and email to me. In your email, please state your name, position, institution and a brief purpose of the measurements. If you are a student, please identify your faculty advisor. Please also state that you agree to reference the appropriate literature if you publish the results. I am not interested in receiving co-author credit for the published results, but I expect you to cite the appropriate literature on the method and the data reduction process. Disclaimer:Because of U.S. Department of Energy regulations, I am unable to respond to enquiries from some foreign countries, such as those that are under technical embargo. I apologize for any inconvenience. Results are provided for research purposes only. No guarantees are made about the accuracy of results. |
Back strain gauge |
Easiest way to do data reduction yourself
Use the MATLAB script within this publication:
Prime, M. B., and Hill, M. R., 2006, "Uncertainty, Model Error, and Order Selection for Series-Expanded, Residual-Stress Inverse Solutions," Journal of Engineering Materials and Technology, 128(2), pp. 175-185. preprint (pdf). (LA-UR-05-2597)
Here is the script and some sample files: series.m, C.txt, a.txt, epsilon.txt, P.txt . The sample files are from the bent beam test. The file C.txt already has the elastic modulus included. For that bent beam, E was 194 GPa and nu was 0.28 so E' = 210.5 GPa. If you wish to compare with the Lee/Hill compliances below, know that those are for E'=1. So C.txt ~ CLee-Hill /210,500MPa * 106 strain/microstrain = CLee-Hill * 4.75.
To apply this to a general solution, you will need to have your own data (a.txt and epsilon.txt) and then coefficients that go with those depths. P.txt is just Legendre polynomials for those depths. The necessary coefficients for C.txt for a beam/plate are available in this paper:
Lee, MJ ; Hill, MR, 2007, "Effect of strain gage length when determining residual stress by slitting," J. Engineering Materials and Technology, 129(1), 375-382. Note: because of rounding errors, the coefficients in that paper will not give accurate results. Corrected coefficients are given in this erratum published in JEMT. Download the coefficients at this page from Mike Hill. Please reference the original publication and the erratum if you use these coefficients.
The 3D paper gives a simple correction to compliances for 3D effects. In the bent beam example, the beam is 10 mm wide and 30 mm deep, so B=1/3, and the correction factor in the paper (Eq 28) is 1.069. The plane-strain compliances in the example should be multiplied by this factor.
For more complicated cases than a back face strain gauge, see the FAQ for learning general calculations.
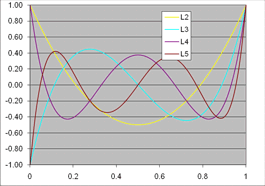
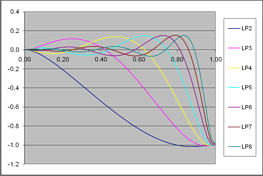
For your reference, here is what typical compliance functions (C, calibration coefficients) look like:
For Legendre polynomials like this through the thickness (these are the stresses or P's) |
The Compliances for a gage opposite the cut (back face) look like this. |