Actinides Under Extreme Pressures

Actinide bonding

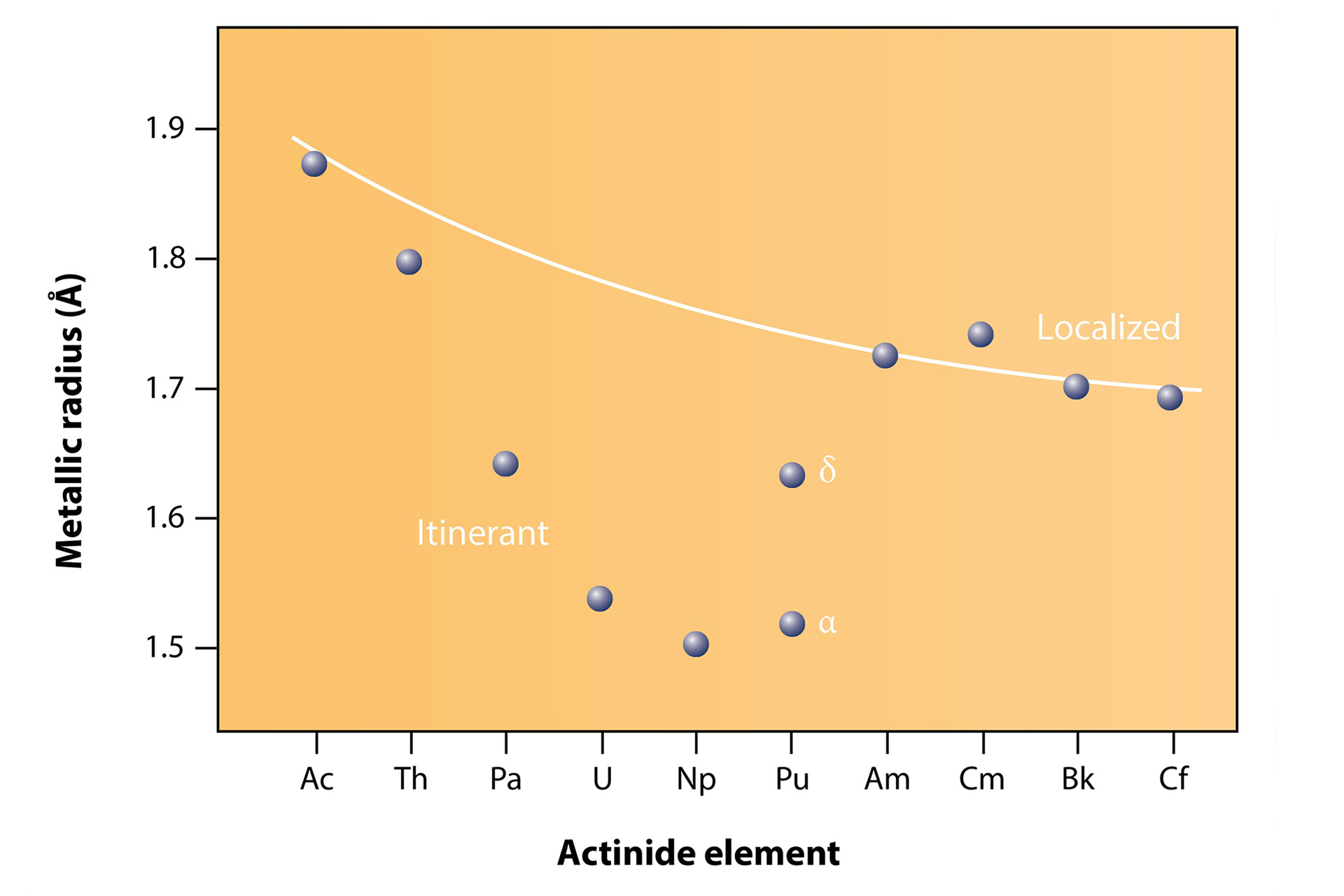
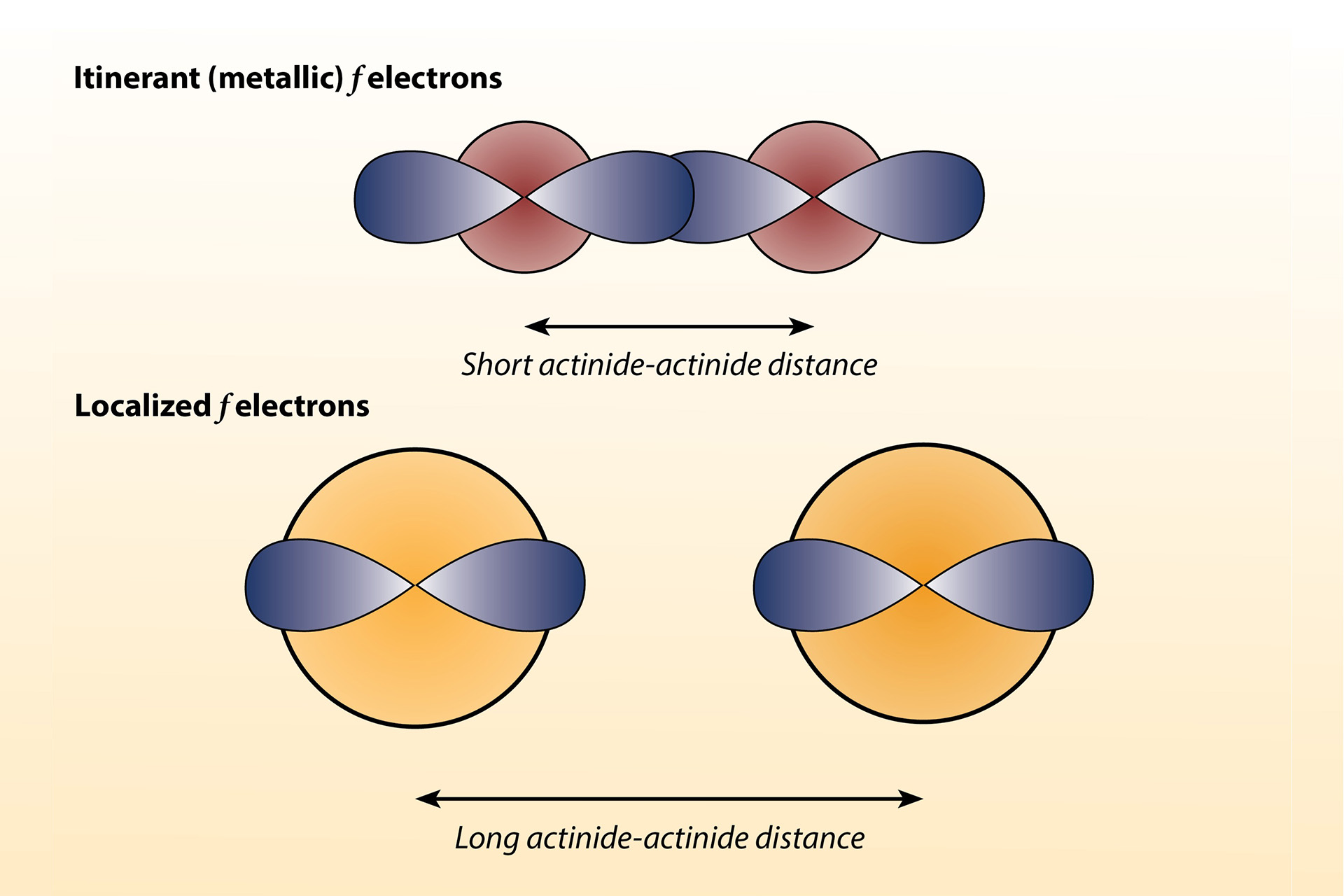
Hill plots

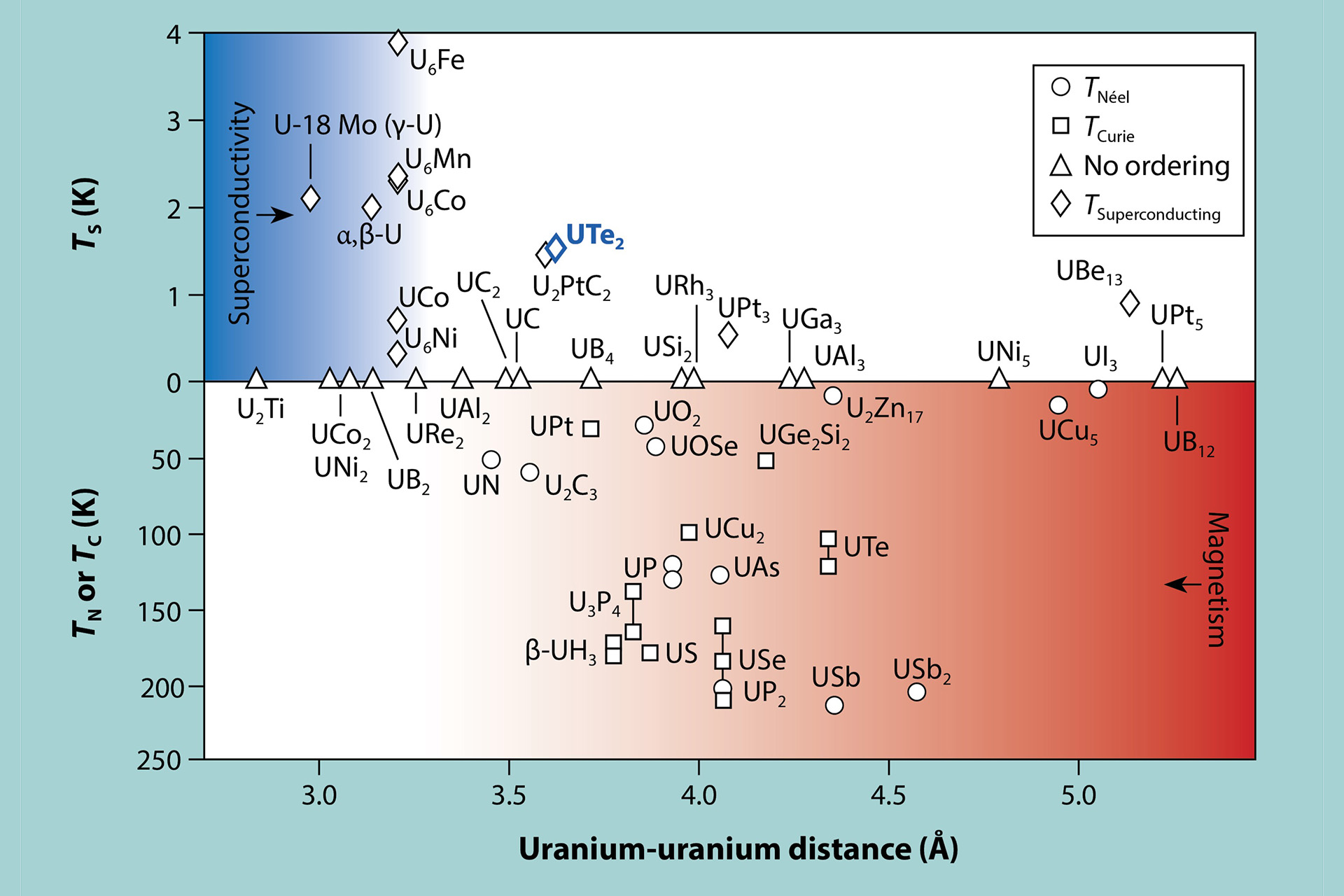
Uranium ditelluride

At ambient pressure, the crystal structure of uranium ditelluride is known to be orthorhombic with an Immm space group. We were interested in how this structure changes with pressure, and therefore chose to use diamond anvil cells coupled with angle-dispersive X-ray diffraction, which can be used to determine changes in crystal structure.

Reaching high pressures

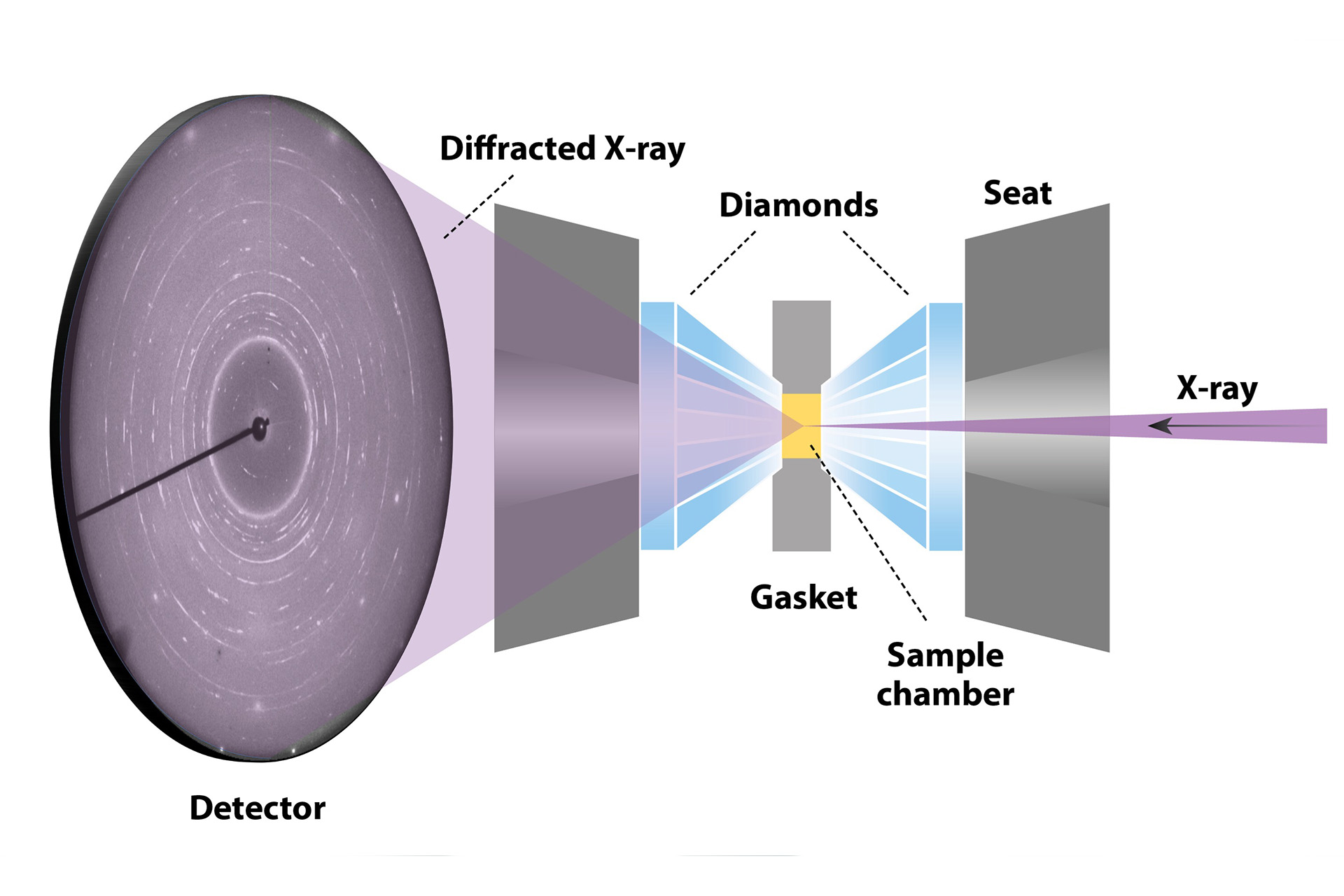
A diamond anvil cell is a small but powerful device that is used to compress samples to ultrahigh pressures (a schematic is shown in Fig. 4). In a typical experiment, a sample is placed between two diamonds in a chamber that is made by drilling a hole in a metal gasket. The diamonds are held in place using seats made from cubic boron nitride, which is X-ray transparent, allowing X-rays to pass through. This optical transparency is a key factor that distinguishes the diamond anvil cell from other pressure devices, allowing material properties to be gauged while under compressive force. Increasing the pressure in a diamond anvil cell is achieved by pushing the diamonds together with opposed uniaxial force. Each diamond has a very small flat tip, known as a “culet,” so that a minimal amount of force can be used to generate significantly high pressures. Pressures greater than those at the center of the Earth can be attained using the diamond anvil cell (approximately 360 GPa).

X-Ray diffraction

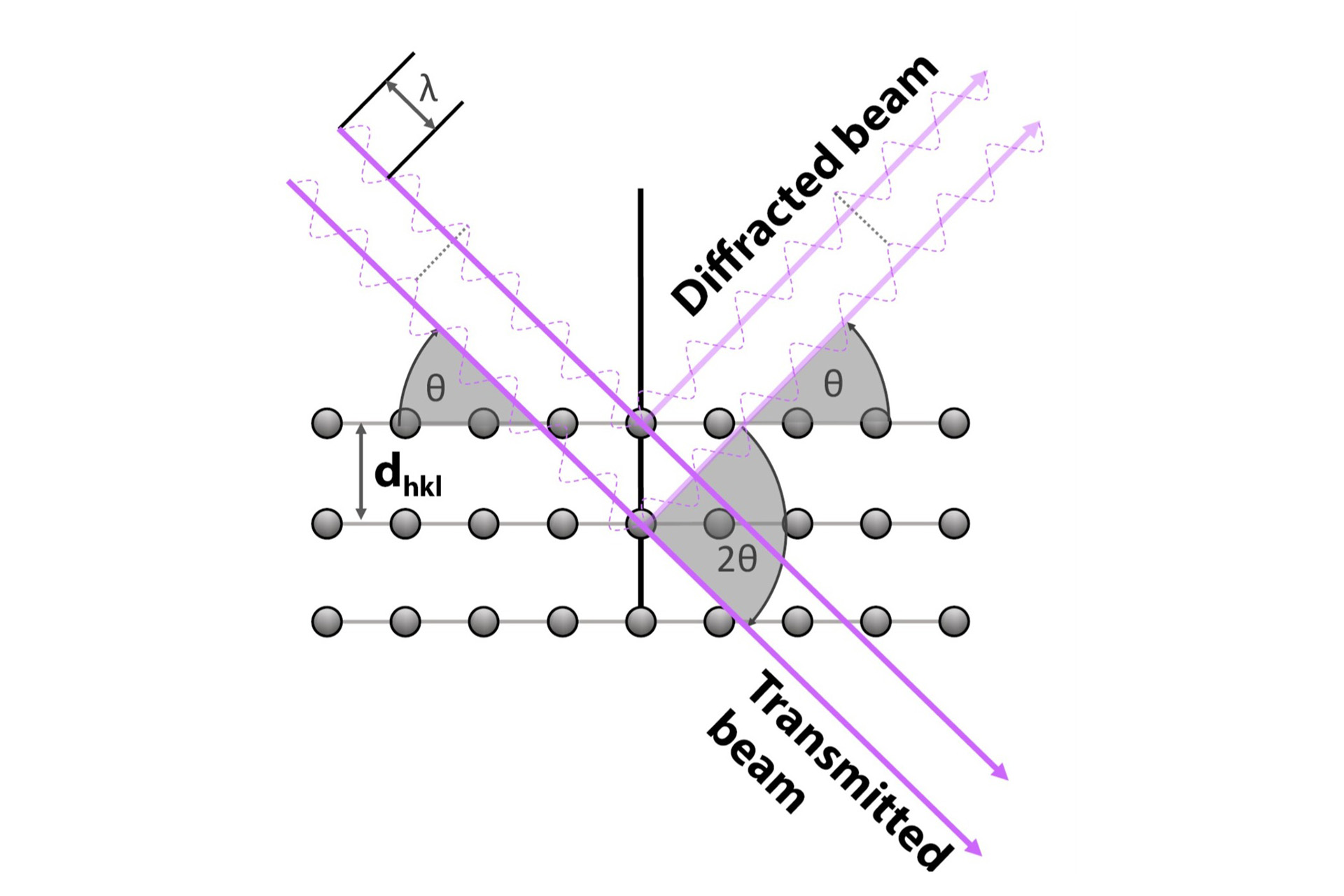
X-ray diffraction can be used to determine the way atoms are arranged in a material in a repetitive 3D pattern—i.e., a crystal structure. In the case of uranium ditelluride, this allows for the density, uranium-uranium distance, and changes in the crystal structure to be determined. X-ray diffraction involves passing a beam of X-rays through a material and observing how the radiation scatters off the material. At an incidence angle θ, the reflected X-rays constructively interfere with X-rays that reflect off other parallel planes, strengthening these signals that can be measured. The scattering of X-rays is described using Bragg’s law (see Fig. 4 for a diagram of the different variables).

The material studied is a powder constituted of multiple small particles which are oriented differently from each other. Each of these grains will therefore have different sets of parallel planes of atoms that satisfy Bragg’s law. The angle of diffraction θ can then be used to determine the difference between atomic planes and calculate the crystal structure of uranium ditelluride. Different crystal structures will have different spacings between the parallel planes of atoms. This allows X-ray diffraction to be used to identify a crystal structure.

Uranium ditelluride under high pressure

An example of an X-ray diffraction image of uranium ditelluride in the diamond anvil cell is shown in Fig. 6a. This image is composed of multiple concentric rings with each ring representing a different set of parallel planes of atoms that diffracts X-rays at an angle of 2θ. Integrating these diffraction patterns around the rings gives the 1D diffraction patterns shown in Fig. 6b.

At 0 GPa, uranium ditelluride has an orthorhombic crystal structure, meaning that the atoms are arranged within a rectangular prism where all sides have different lengths and are perpendicular to each other. Fig. 6c shows how the uranium and tellurium atoms are arranged within the orthorhombic unit cell, where the unit cell is the repeating unit that makes up the crystal structure. Given that the dimensions of the unit cell are not equal, there are many different spacings between different parallel planes of atoms, resulting in a large number of peaks in the 1D diffraction pattern. The peaks corresponding to the orthorhombic structure are indicated by blue triangles in Fig. 6b.

When the pressure was increased to 6 GPa, the peaks from the orthorhombic structure decrease in intensity and additional peaks appear. These peaks indicate that the atoms in the orthorhombic structure have shifted positions to form a new crystal structure. In this case, the new crystal structure is a tetragonal structure with an I4/mmm space group, where the atoms repeat in a square prism unit cell with two equal and one unequal sides (Fig. 6c). At this pressure, both the orthorhombic and tetragonal structures are present. At 8 GPa, only the latter is present, meaning that all the atoms have rearranged themselves into the tetragonal structure. The new structure of uranium ditelluride remains present when pressure is decreased down to atmospheric pressure (this change in crystal structure is known as a phase transition). As the arrangement of atoms is different in the tetragonal phase, the uranium-uranium distance changes and therefore the interactions between the 5f electrons and the uranium atoms are different. The material slowly reverts to the orthorhombic phase approximately 2–3 weeks after being decompressed to ambient pressure.

Compressibility hints

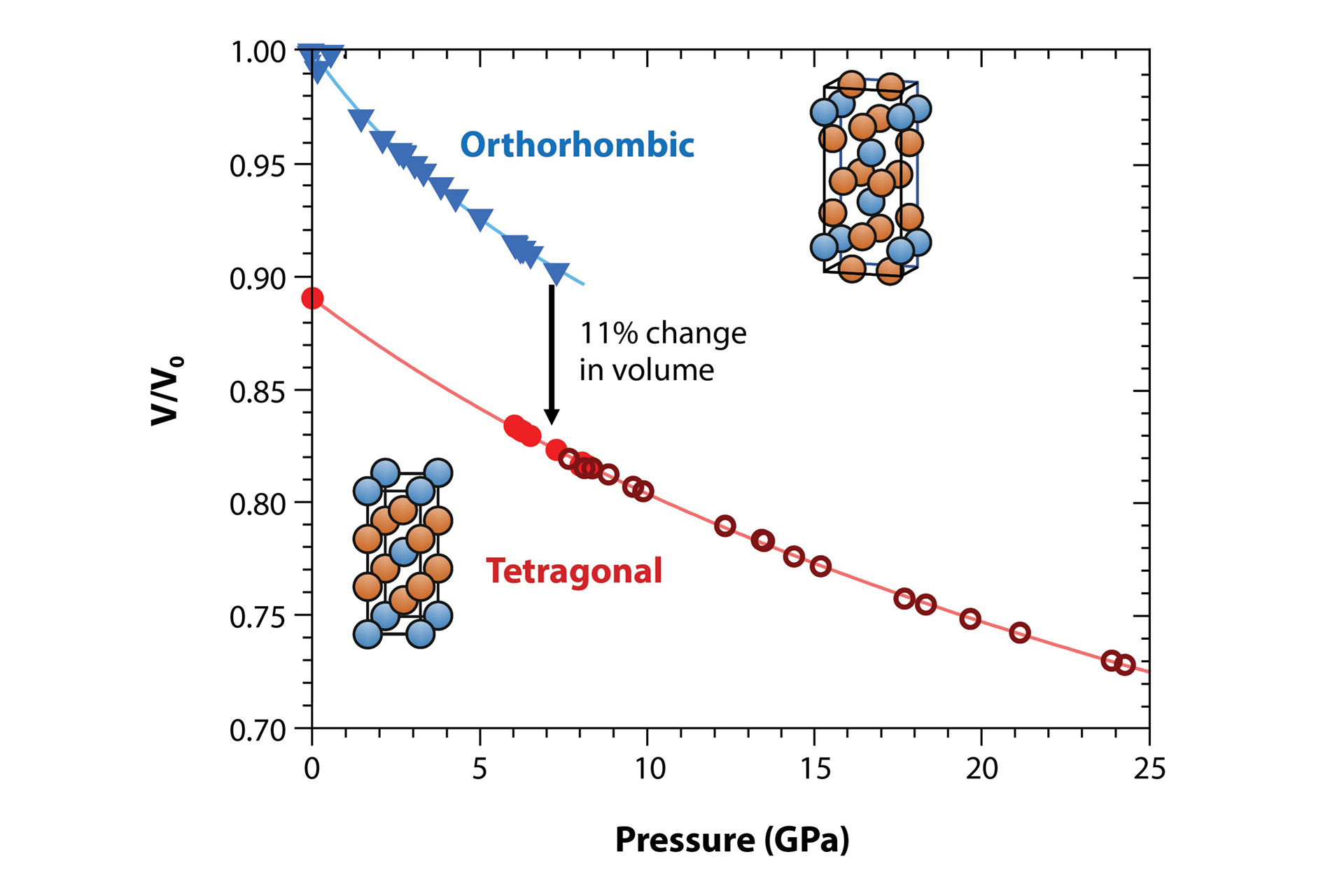
The bulk modulus is a quantity that measures a material’s resistance to being compressed. A material with a high bulk modulus such as diamond is difficult to compress while a material with a low bulk modulus such as a sponge is easier to compress. However, as a sponge is compressed, it becomes more difficult to further compress the smaller it becomes. This means that the bulk modulus changes in a material under compression, therefore, the change in bulk modulus with pressure is an important value to quantify.

When a material is compressed, its unit cell typically becomes smaller as atoms are pushed closer together, meaning that the same atoms occupy a smaller volume. The pressure-volume relationship can be modeled to give the bulk modulus and how it changes with pressure, known as an equation of state. If a bulk modulus is small, the volume decreases at a faster rate. The solid lines in Fig. 7 show the fit of the equation of state to the data. With this fit, we find that at ambient pressure (0 GPa), the orthorhombic phase shows a bulk modulus of 46 GPa, versus 79 GPa for the tetragonal phase. This means that at ambient pressure, the tetragonal phase is more difficult to compress than the orthorhombic phase.

Determining the bulk modulus is important because it can give us hints about why uranium ditelluride undergoes a phase transition at high pressure. This is due to the relationship between the bulk modulus, the complexity of the crystal structure (symmetry), and the bonding of the electrons. In compounds where the bulk modulus is lower for the low-pressure phase (e.g., uranium telluride, UTe), the change in crystallographic phase was explained by a mixed-valence state. The accompanying change in bulk modulus is due to this change in crystal structure—for example, graphite is soft and easy to compress but if you phase-transform it to diamond, it becomes difficult to compress. Uranium ditelluride has similar behavior to uranium telluride, where the phase which is more resistant to compression is observed, i.e., the one with a higher bulk modulus. In the case of uranium ditelluride, this is the tetragonal structure, suggesting that a mixed-valance state is present in orthorhombic uranium ditelluride, which has been reported in the literature.

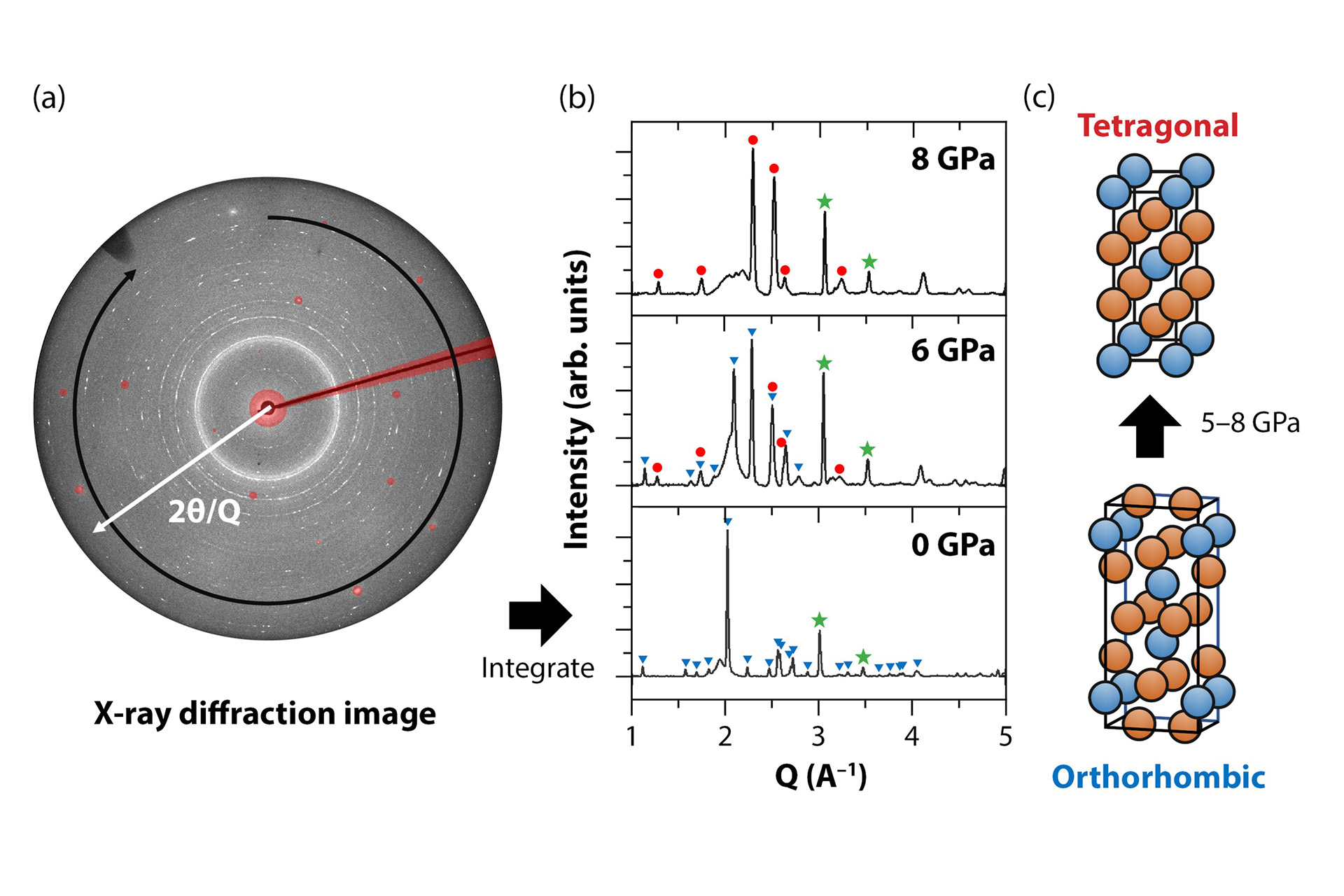
Additional peaks (green stars) are from the copper that was used to determine the pressure. (c) The orthorhombic and tetragonal structures of uranium ditelluride.

Summary

High-pressure X-ray diffraction was performed on uranium ditelluride, a uranium intermetallic compound with recently discovered superconducting properties that vanish at high pressures. At these pressures, we found that it undergoes a phase transformation from its ambient orthorhombic structure to a tetragonal structure, beginning at 6 GPa and completing the transformation at 8 GPa. The difference in the bulk modulus of the two phases and the transition to a simpler crystal structure with greater uranium-uranium distances and high symmetry suggests that the phase transition is likely due to an increased localization of the 5f electrons.

Acknowledgments

Funding of this work was provided by the Seaborg Institute. Beamtime access was provided by the High-Pressure Collaborative Access Team (HPCAT) at Argonne National Laboratory, which is funded by the DOE and NNSA. The author would like to thank Blake Sturtevant and Eric Bauer for their mentorship and Priscilla Rosa, Ashley Weiland, Brian Scott, and Dmitry Popov for their contributions to this work.

Further reading:

1. L.Q. Huston, D.Y. Popov, A. Weiland, M.M. Bordelon, P.F.S. Rosa, R.L. Rowland, II, B.L. Scott, G. Shen, C. Park, E.K. Moss, S.M. Thomas, J.D. Thompson, B.T. Sturtevant, E.D. Bauer, “Metastable phase of UTe2 formed under high pressure above 5 GPa,” Phys. Rev. Materials, 6, 2022, 114801.
2. S.M. Thomas, F.B. Santos, M.H. Christensen, T. Asaba, F. Ronning, J.D. Thompson, E.D. Bauer, R.M. Fernandes, G. Fabbris, P.F.S. Rosa, “Evidence for a pressure-induced antiferromagnetic quantum critical point in intermediate-valence UTe2,” Sci. Adv., 6, 2020, eabc8709.
3. J.A. Mydosh, P.M. Oppeneer, “Hidden order behaviour in URu2Si2,” Philos. Mag., 94, 2014, 3642.
4. N. Shekar, V. Kathirvel, B. Shukla, P. Sahu, “Phase transitions and structural stability of binary uranium intermetallics under high pressure: A review,” Proc. Natl. Acad. Sci. India A, 82, 2012, 163.
5. J.M. Léger, I. Vedel, A.M. Redon, J. Rossat-Mignod, O. Vogt, “High pressure X-ray studies of UAs and UTe,” Solid State Commun., 66, 1988, 1173.
6. S. Ran, S.R. Saha, I.L. Liu, D. Graf, J. Paglione, N.P. Butch, “Expansion of the high field-boosted superconductivity in UTe2 under pressure,” npj Quantum Mater., 6, 2021, 75.
7. S. Ran, C. Eckberg, Q-P. Ding, Y. Furukawa, T. Metz, S.R. Saha, I-L. Liu, M. Zic, H. Kim, J. Paglione, N.P. Butch, “Nearly ferromagnetic spin-triplet superconductivity,” Science, 365, 2019, 684.
8. A.M. Boring, J. Smith, “Plutonium condensed-matter physics,” Los Alamos Science, 26, 2000, 90.