
Image Caption: On the left is the electron density from a simulation for deuterium at 10 g/cc and 10 eV. On the right is the electron density for carbon at 5.7 g/cc and 8.62 eV.
Determining the fundamental properties of plasmas (e.g., equation of state, transport properties) over a wide range of temperatures and densities poses a significant challenge.
In these conditions of elevated temperature and density relative to the ambient condensed matter state, ions can be strongly coupled and electrons are at least partially degenerate, requiring a quantum treatment. These conditions have proven difficult to describe theoretically and necessitate numeric simulations.
One key approach is quantum molecular dynamics simulations. In this approach, the ions are treated classically and propagated according to Newton’s equations where the force is determined from the ions' interaction with each other and the electron density. The electron density is solved for at each ionic configuration according to the Born-Oppenheimer approximation. Density functional theory (DFT) is a formally exact method to determine the electron density of quantum electrons without reference to the many body wave equations.
Despite this success, as temperatures lower, Thomas-Fermi quickly loses accuracy. To achieve high accuracy, one may include corrections based on not just the local density but on the local gradient of density as well. Perrot derived the first order correction at finite temperature in the formal expansion for a slowly varying density; this improves results moderately. Generalized gradient approximations have further improved results though have not been able to reproduce Kohn-Sham DFT results, which is the benchmark for orbital-free DFT where it can be calculated, across density and temperature regimes.
[Image Diagram]
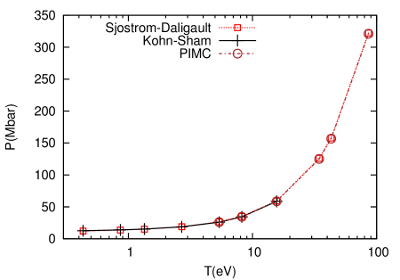
We have developed a non-local (i.e., depends on two points in space) functional by requiring a correct limit of the density-density response of the electron gas, which cannot be attained with local functionals. This has yielded highly accurate results across temperature regimes. Specifically, it is in very good agreement with Kohn-Sham methods from low to moderately high temperature, and above where Kohn-Sham calculations can be done, it is in very good agreement with highly accurate path integral Monte Carlo calculations. Results are shown here for deuterium at 4.05 g/cc. Continued work is ongoing for application to heavy element systems as well as mixtures.



