The Warm Dense Matter Regime
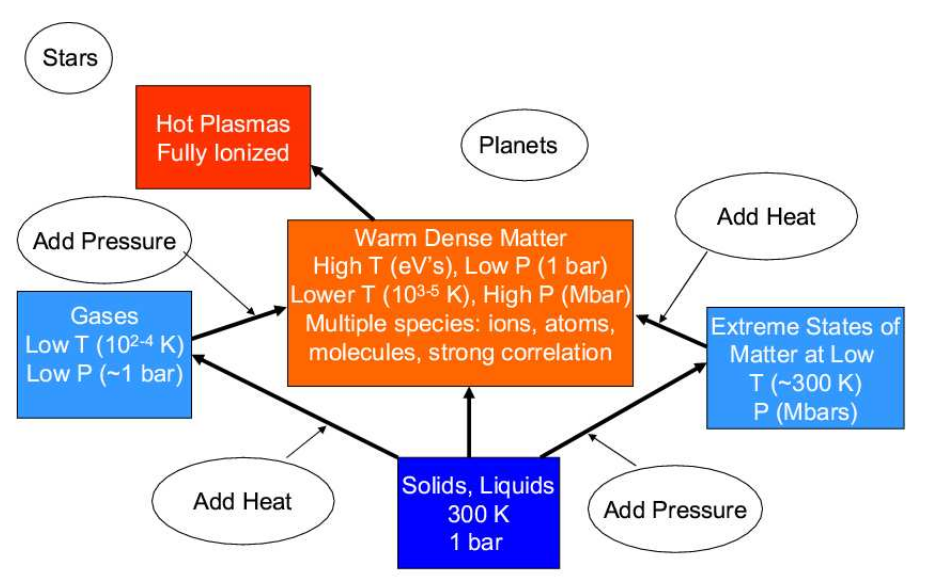
Warm dense matter composes a condensed matter regime characterized by a wide range of electron temperatures \(T \sim 1 - 100 \) eV and pressures from ambiant to many Mbar. The relationship between the warm dense matter regime and other states of matter is illustrated schematically in the figure above, while below, a generalized phase diagram depicts the warm dense matter region.
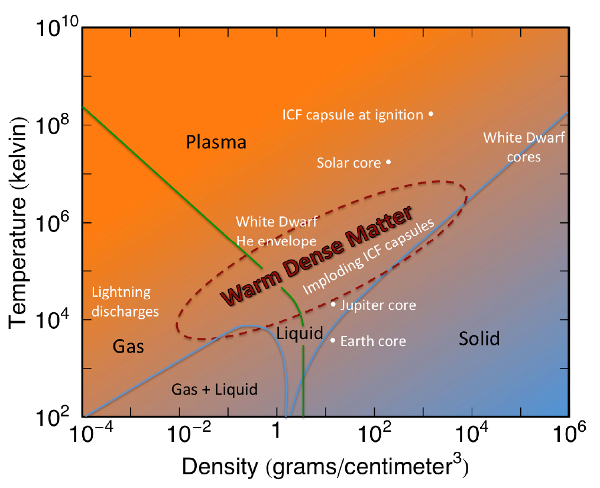
Recently, warm dense matter has attracted attention because of its importance in diverse physical systems, including exo-planet interiors, the path to inertial confinement fusion, and neutron stellar atmospheres, as well as because of increased accessibility through large-scale laboratory experiments. For example, facilities such as the Linac Coherent Light Source (LCLS) have significant advancements in X-ray free-electron lasers (XFELs), allowing for pump and probe capabilities that provide unprecedented means to generate and study material properties in warm dense matter conditions. In particular, with spectrally resolved X-ray scattering, detailed measurements of the electron densities, temperatures and ionization states of compressed materials are now being achieved, which allows for cross validation between theoretic/computational predictions and the experiments themselves.
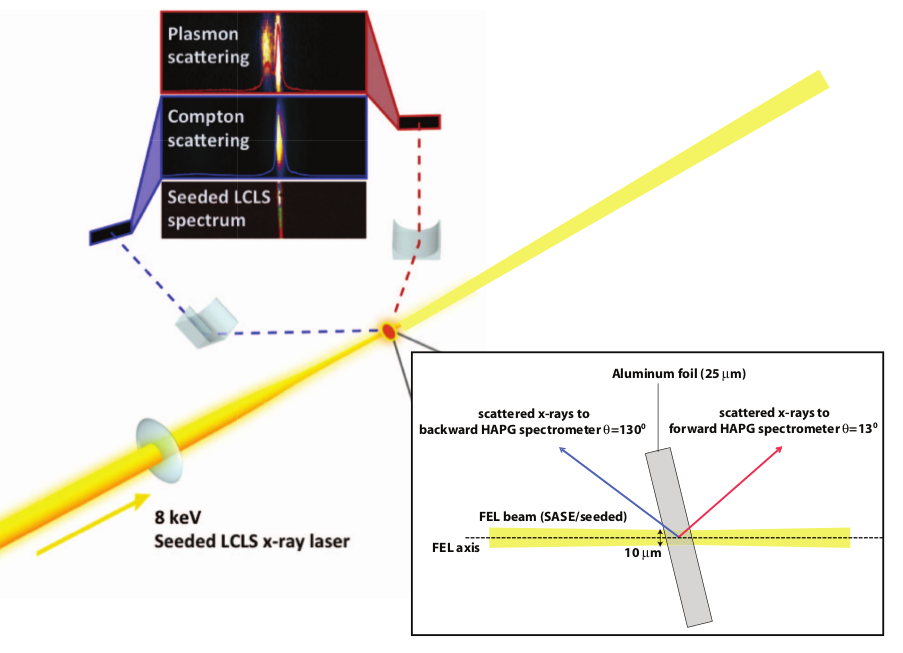
A schematic of LCLS X-ray scattering experiment on solid aluminum.
The regime is inherently challenging because its thermodynamics cannot be framed in terms of small perturbations from ideal, solvable models. Warm dense matter temperature and pressure ranges correspond to values of order unity in the two relevant expansion parameters: the Coulomb coupling parameter \( \Gamma \) and the electron degeneracy parameter \( \Theta \). Warm dense matter thus does not fall neatly within the parameter space typical of either ordinary condensed-matter physics or plasma physics. One result is that plasma physics methods, which originate in the classical limit, do not extend well into the warm dense matter regime, where quantum effects for the electrons must be considered.
Conversely, condensed-matter physics methods must be extended well beyond their normal realms of application. A foundational element for understanding dense plasmas is the equation of state (EOS). For materials under near-ambient conditions, best practice has evolved to be a combination of electronic structure calculations using density functional theory (DFT) and molecular dynamics (MD). In its simplest form, Born-Oppenheimer MD gets the electronic forces on the nuclei (or ions) from a DFT calculation at each nuclear step and then moves the ions according to classical Newton's equations, thereby combining chemical realism from explicit quantum mechanical treatment of the electrons with the classical contributions of the nuclear species. Though highly successful in the traditional low-temperature condensed matter phase, at higher temperatures the standard approach of Kohn-Sham DFT becomes prohibitive and alternative formulations must be used.
References
- Basic Research Needs for High Energy Density Laboratory Physics, Report on the Workshop on High Energy Density Laboratory Physics Research Needs, Nov. 15–18, 2009
- Frontiers and Challenges in Warm Dense Matter, Lecture Notes in Computational Science and Engineering Vol. 96 (Springer, Berlin, 2014)
- University of Florida, Density functional theory for warm dense matter, Website
- LCLS Matter in Extreme Conditions