The Physical Regimes
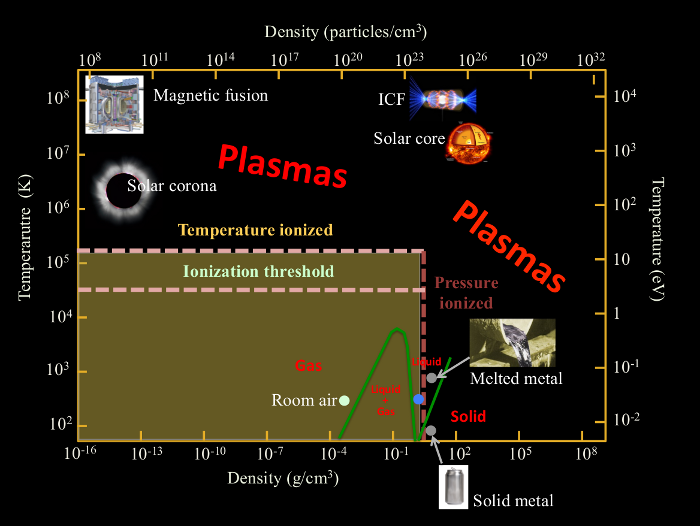
Plasmas of interest to this project span a wide region of phase space in terms of density and temperature and require theoretical understanding from both traditional (classical) plasma physics as well as condensed matter (quantum) physics. For example, we may consider the low temperature case of nearly free valence electrons of solid aluminum, or the high temperature case of fully ionized hydrogen near fusion ignition. Two parameters can, in general, describe our systems: the Coulomb coupling parameter and the degeneracy parameter.
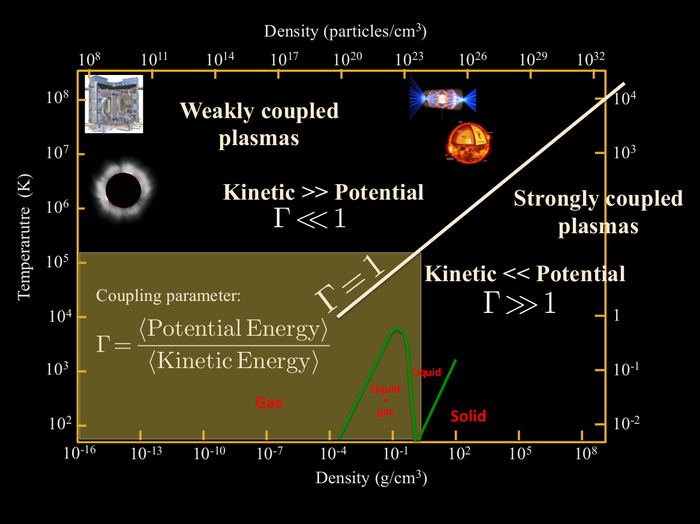
Coulomb coupling strength
The Coulomb coupling parameter \[\Gamma=\frac{\langle E_{potential}\rangle}{\langle E_{kin}\rangle}\] is defined as the ratio of the mean potential energy per particle to the mean kinetic energy per particle. It measures the degree to which many-body interactions affect the dynamics of particles in the system. When \( \Gamma << 1\), the system is weakly coupled: particles have enough kinetic energy to cruise through the system (the ideal gas limit corresponds to \(\Gamma=0\)). When \( \Gamma >> 1\), interparticle interactions strongly affect the behavior of individual particles: the system is strongly coupled.
For a system of ions of charge \(Ze\) at density \( n\) and temperature \(T\), \(\Gamma \equiv (Ze)^2/(a k_B {\rm T})\) with \(a=(3/4\pi n)^{1/3}\) is the Wigner-Seitz radius and \(k_B =\) Boltzmann constant.
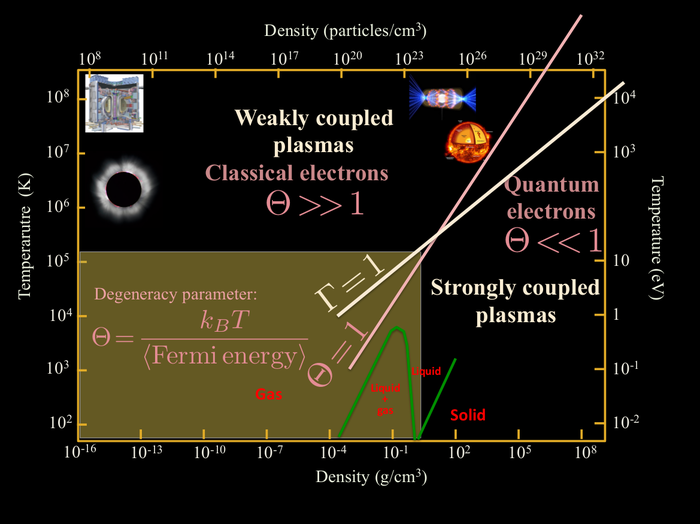
Degeneracy parameter
Conduction electrons in a plasma can no longer be described by classical, point particles when their typical, average deBroglie wavelength known as the thermal deBroglie wavelength \( \lambda_{dB}=\frac{\hbar}{(2mk_BT)^{1/2}} \) is no longer small compared with the average interparticle distance \(\Delta x\) between electrons.
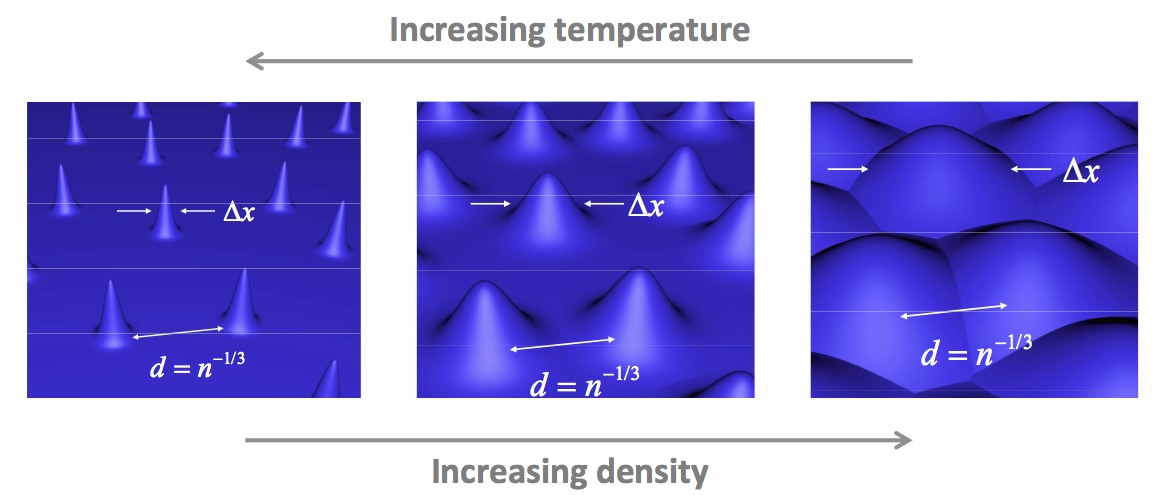
This occurs at high density when electrons get closer to each other or at low enough temperature, in which case the thermal wave-length increases and wave packets increasingly overlap. Equivalently, this happens when the degeneracy parameter \[\Theta=\frac{k_B T}{E_F}\sim\left(\frac{\lambda_{dB}}{a}\right)^{-2} \] defined as the ratio of the thermal energy \(k_B T\) over the Fermi energy \(E_F=\frac{\hbar^2}{2m}(3\pi^2n)^{2/3}\) is less than unity. For \( \theta >>1\), the system is non-degenerate and quantum effects can be neglected (*). For \( \theta <<1\) the system is degenerate and quantum effects are important. In particular, quantum mechanics must be used to describe the dynamics of electrons, and one needs to account for the fermionic nature of electron: the Boltzmann statistics \(n_{B}(\epsilon)=e^{(\mu-\epsilon)/k_BT}\) of single-particle states must be replaced with the Fermi-Dirac statistics \[ n_{FD}(\epsilon)=\frac{1}{1+e^{-(\mu-\epsilon)/k_BT}}\,,\]where \(\mu\) is the chemical potential. In the classical limit, \( \Theta\!>\!>\!1 \) , \( \mu/k_BT\to-\infty\) and \(n_{FD}\to n_{B}\). The effects of the quantum statistics are illustrated in the graphics below.
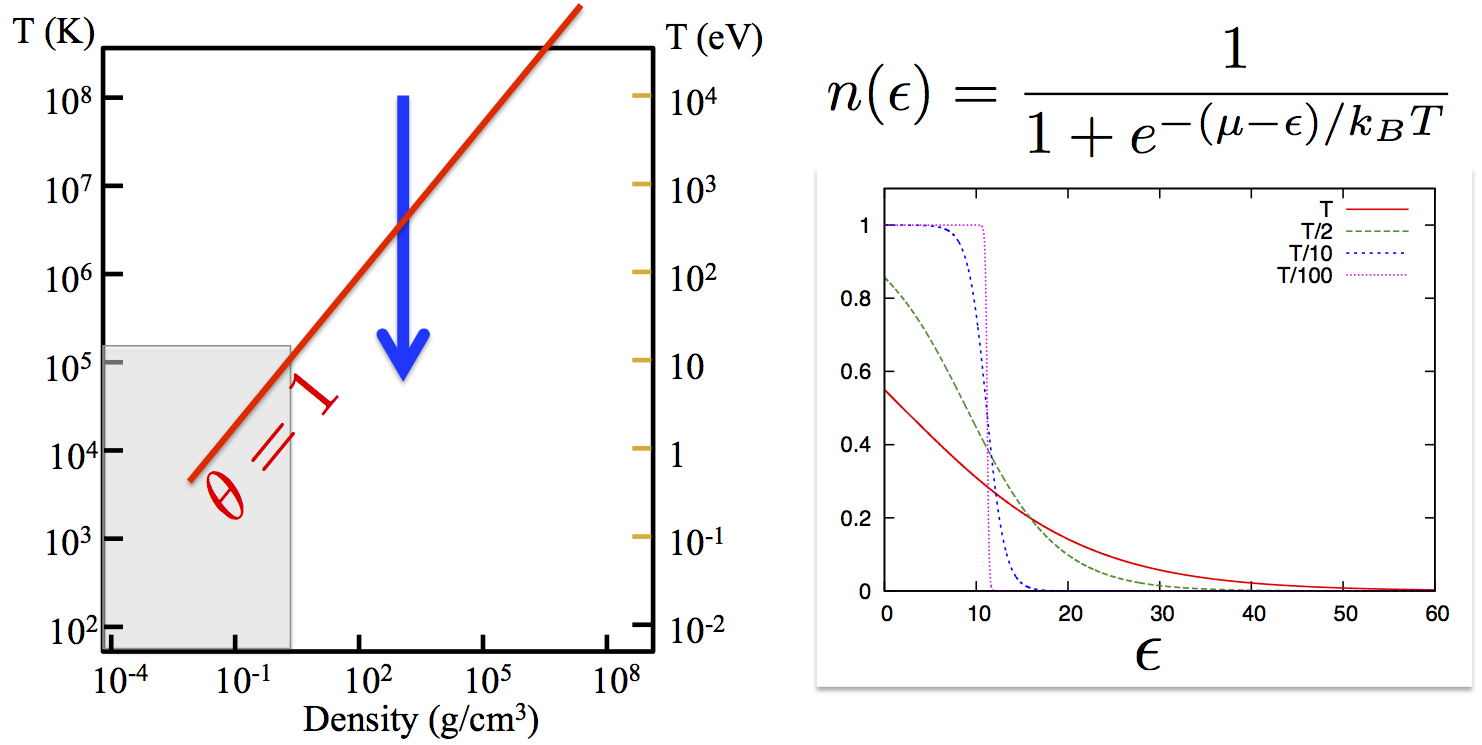
Lowering the temperature at constant density, the distribution of energy levels transitions from a smooth, widespread Boltzmann distribution to an increasingly steeper distribution at very low temperature. This affects the electron collisionality due to the Pauli blocking of electronic transitions.
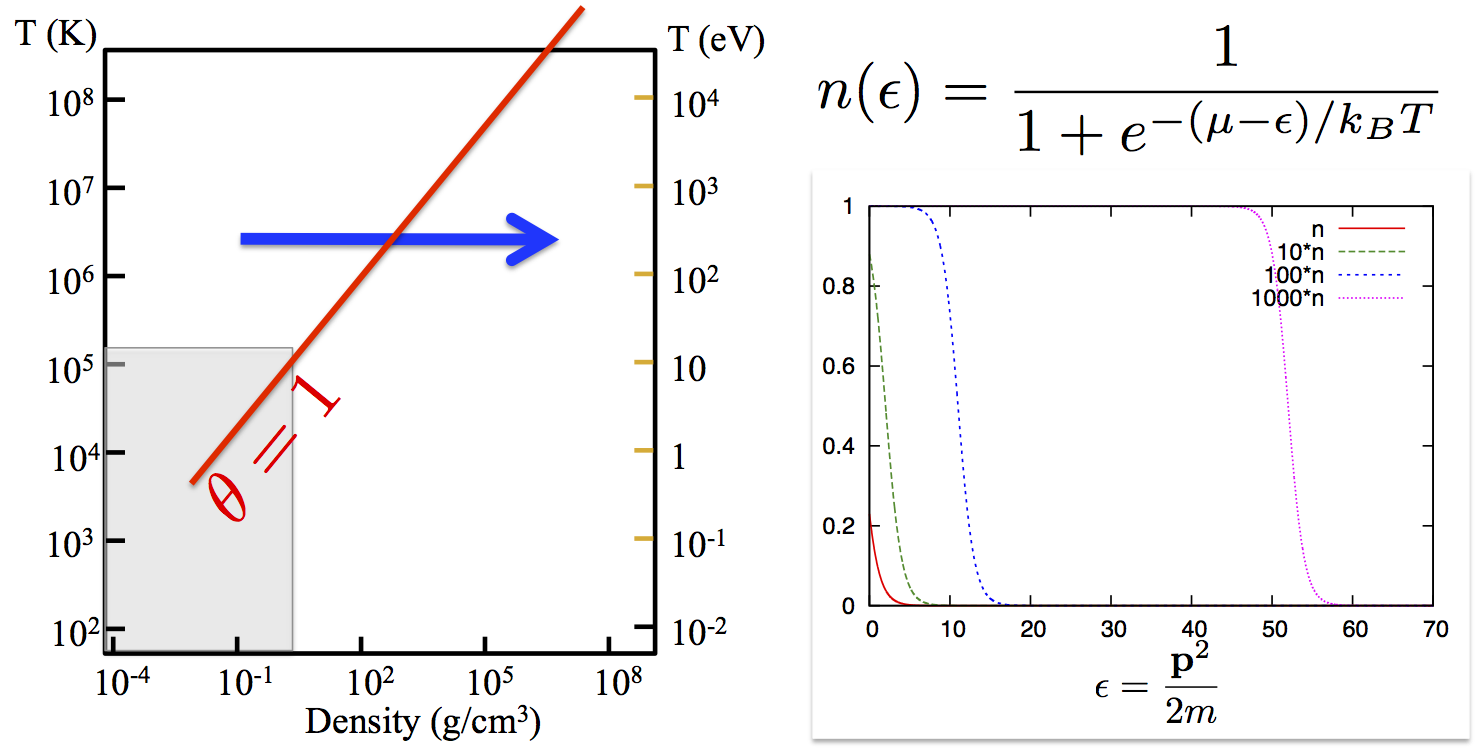
Increasing the density at constant temperature, the number of high-energy states increases and the distribution approaches a step function. This effect leads to the Fermi pressure responsible for the stability of old stars.
Note that, even in classical plasmas with \(\Theta>\!>1\), the rare close collisions between electrons and ions are almost always quantum mechanical because \( \lambda_{dB}>r_c=\frac{Ze^2}{k_BT} \), where \(r_c\) is the distance of closest approach between an electron and an ion of charge \(Ze\).
The regime where both \( \Gamma \) and \( \theta \) are near unity is one definition of so-called warm dense matter. This region is of particular difficulty for theoretic and computational methods because approximations of traditional plasma physics are no longer valid and methods of lower temperature condensed matter, such as Kohn-Sham density functional theory, become computationally prohibited.