Figure 1: Global indexes for four vertices associated with cell (i, j, k)
.
![\includegraphics[bb=171 117 470 641,scale=.6]{/home/hall/Caesar/documents/images/Augustus/Morel/sofig1.eps}](img17.gif)
![\includegraphics[bb=171 117 470 641,scale=.6]{/home/hall/Caesar/documents/images/Augustus/Morel/sofig1.eps}](img17.gif)
Figure 2: Local and global indices for three of six face centers associated
with cell (i, j, k)
.
![\includegraphics[bb=171 99 470 650,scale=.5]{/home/hall/Caesar/documents/images/Augustus/Morel/sofig2.eps}](img18.gif)
![\includegraphics[bb=171 99 470 650,scale=.5]{/home/hall/Caesar/documents/images/Augustus/Morel/sofig2.eps}](img18.gif)
Figure 3: Local and global indices for three of six face centers associated
with cell (i, j, k)
.
![\includegraphics[bb=171 99 470 669,scale=.5]{/home/hall/Caesar/documents/images/Augustus/Morel/sofig3.eps}](img19.gif)
![\includegraphics[bb=171 99 470 669,scale=.5]{/home/hall/Caesar/documents/images/Augustus/Morel/sofig3.eps}](img19.gif)
Figure 4: Vertex shared by the Right, Top, and Up faces having local index RTU.
![\includegraphics[bb=198 239 456 587,scale=.6]{/home/hall/Caesar/documents/images/Augustus/Morel/sofig4.eps}](img20.gif)
![\includegraphics[bb=198 239 456 587,scale=.6]{/home/hall/Caesar/documents/images/Augustus/Morel/sofig4.eps}](img20.gif)
where
where |
| = | |||
| = |
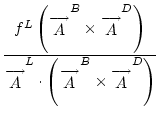 +
+
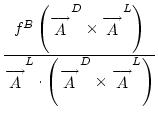 +
+ 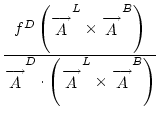 .
.
where a superscript ``t'' denotes ``transpose.'' The three face-area components associated with the Right-Top-Up vertex are illustrated in Fig.4. The algebraic flux vectors for the other vertices are defined analogously.
where f is the face index and the sum is taken over all faces.
where v is the vertex index, and Vv denotes the volumetric weight associated with vertex v .
VLBD = 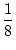
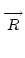 1, 2 x
1, 2 x 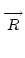 1, 3 .
1, 3 . 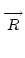 1, 4 ,
1, 4 ,
where
where
and
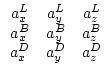
where aLx denotes the x-component of the area vector associated with the left face. The remaining components of the matrix are defined analogously.
where
S = AtA ,
and the dot product is taken in the usual way.
where the sum is taken over all faces.
W-1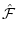 =
= 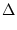
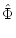 ,
,
where
and
while requiring continuity of the flow yields:
- fRi, j, k - fLi+1, j, k = 0 ,
where V denotes the total cell volume, QC denotes the cell-center inhomogeneous source, and the cell index (i, j, k) has been supressed for simplicity.
- fRi, j, k - fLi+1, j, k = 0 .
- fR0, j, k - fL1, j, k = 0 ,
where
- fR0, j, k = 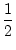 |
|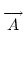 |L1, j, k
|L1, j, k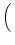
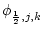 -
- 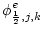
 ,
,
where