

Next: Derivation of the Discretization
Up: Morel99b
Previous: Properties of the Scheme
We next describe the support-operators method. It is convenient at this point to define a flux operator given by
- D . The diffusion operator of interest is given by the product of the divergence operator and the flux operator:
-
. The diffusion operator of interest is given by the product of the divergence operator and the flux operator:
- 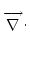 D
D . The support-operator method is based
upon the following three facts:
. The support-operator method is based
upon the following three facts:
- Given appropriately defined scalar and vector inner products, the divergence
and flux operators are adjoint to one another.
- The adjoint of an operator varies with the definition of its associated inner
products, but is unique for fixed inner products.
- The product of an operator and its adjoint is a self-adjoint positive-definite
operator.
The adjoint relationship between the
flux and divergence operators is embodied in the following integral
identity:
where 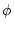 is an arbitrary scalar function,
is an arbitrary scalar function,
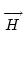 is an arbitrary vector
function, V
denotes a volume,
is an arbitrary vector
function, V
denotes a volume,
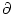 V
denotes its surface, and
V
denotes its surface, and
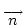 denotes the outward-directed unit normal associated with that surface.
denotes the outward-directed unit normal associated with that surface.
Our support-operator method can be described in the simplest terms as follows:
- Define discrete scalar and vector spaces to be used in a discretization of the integral identity.
- Fully discretize all but the flux operator in the identity over a
single arbitrary cell. The flux operator is left in the general form
of a discrete vector as defined in Step 1.
- Solve for the discrete flux operator (i.e., for its vector
components) on a single arbitrary cell by requiring that the discrete version of
the identity hold for all elements of the discrete scalar and vector spaces defined in Step 1.
- Obtain the interior-mesh discretization of the identity by connecting adjacent mesh cells in such a way as to ensure that the identity is satisfied over the whole grid. This simply amounts to enforcing continuity of intensity and normal-component flux at the cell interfaces.
- Change the flux operator at those cell faces on the exterior mesh
boundary so as to satisfy the appropriate boundary conditions.
- Combine the global divergence matrix and the global flux matrix
to obtain the global diffusion matrix.


Next: Derivation of the Discretization
Up: Morel99b
Previous: Properties of the Scheme
Michael L. Hall