THE HYBRID OPTIMIZATION SOFTWARE SUITE
LA-UR-20-30066
At Los Alamos National Laboratory (LANL) researchers have developed a hybrid multi-physics software package called HOSS - the Hybrid Optimization Software Suite. Integrating computational fluid dynamics (CFD), with state-of-the-art combined finite-discrete element methodologies (FDEM) - consisting of finite element analysis (FEA) and discrete element methods (DEM) - into a single simulation platform, HOSS is capable of solving complex problems for a myriad of engineering disciplines, industrial applications, and scientific research. Whether on a personal desktop or high-performance computing clusters, HOSS’ parallelization allows it to efficiently handle millions of interacting and fracturing solids and/or particle systems. HOSS has been recognized as a 2016 R&D top 100 finalist.
Functional Capabilities
In the last decade, scientific application-driven developments of FDEM have taken place at Los Alamos National Laboratory, enabling researchers to shift the boundaries of FDEM solutions towards next-generation algorithms.
Select from the following dropdown windows to learn more.
Lei, Z., Rougier, E., Knight, E.E., Munjiza, A., & Viswanathan, H. 2016. A generalized anisotropic deformation formulation for geomaterials. Comp. Part. Mech 3, 215-228. https://doi.org/10.1007/s40571-015-0079-y
Lei, Z., Rougier, E., Knight, E.E., Frash, L., Carey, J.W., & Viswanathan, H. 2016. A nonlocking composite tetrahedron element for the combined finite discrete element method. Engineering Computations. 33(7), 1929-1956. https://doi.org/10.1108/EC-09-2015-0268
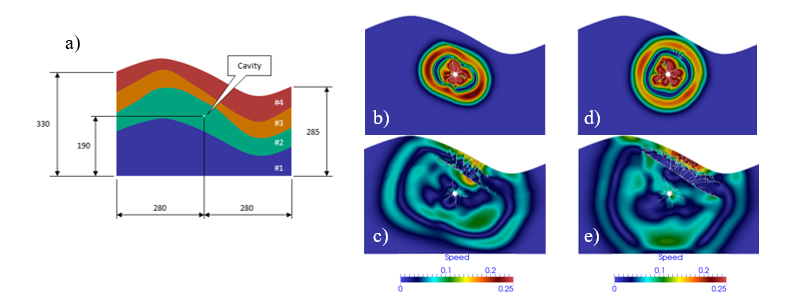
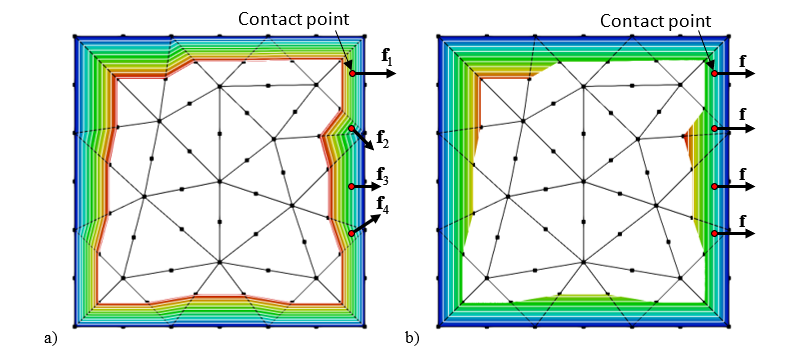
The problem with existing distributed potential contact force algorithms is that the potential field introduces artificial numerical non-smoothness in the contact force, i.e. the contact forces calculated experience a jump (in amplitude and/or direction) when the contact points move from one finite element to another finite element. To overcome this issue, a new solution, which is named the Smooth Contact Algorithm (SCA) was developed in HOSS.
In the SCA, a smooth potential field is introduced according to the global geometry information of each discrete element. In particularly, the SCA calculates contact potential at nodes of the finite element mesh by taking into account nodal connectivity and existing discrete element boundaries. The contact force is then calculated as a function of the gradient of the potential field. Thus, a smooth contact evolution for a smooth surface is recovered.
Lei, Z., Rougier, E., Bryan, E., Munjiza, A. A smooth contact algorithm for the combined finite discrete element method. Computational Particle Mechanics, 2020. https://doi.org/10.1007/s40571-020-00329-2
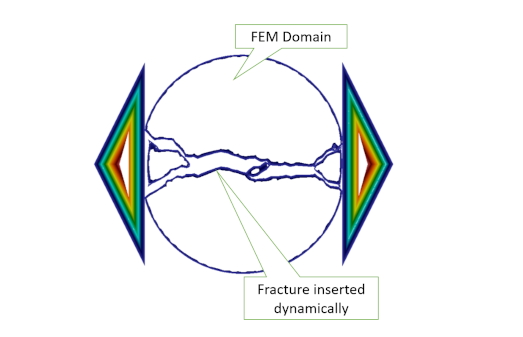
Cohesive Zone Models (CZMs) usually are used to simulate the fracture and fragmentation of solids. Existing CZMs have different disadvantages, such as artificial compliance and time-discontinuity. In order to avoid these drawbacks, the Unified Cohesize Zone Model (UCZM) was implemented into HOSS. In UCZM, damage surfaces are dynamically inserted into the model according to the local stress state, much like the extrinsic CZM approach. However, in order to avoid sudden jumps in the simulations, the state variables are smoothly transitioned from continua to discontinua through an algorithm that properly balances the nodal forces during the process, while maintaining highly efficient simulations.
Lei Z, Rougier E, Knight EE, Munjiza A. A libraries-based multidimensional fracture workbench. US Provisional Patent Application No. 62906674, filed 9/26/2019
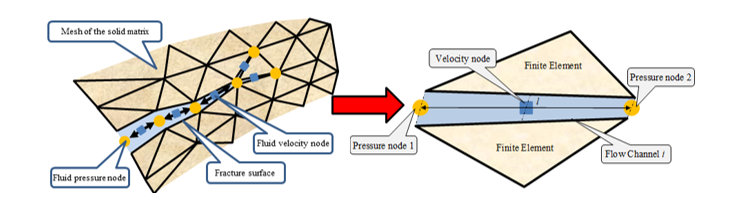
Lei, Z., Rougier, E., Munjiza, A., Viswanathan, H., & Knight, E.E. Simulation of discrete cracks driven by nearly incompressible fluid via 2D combined finite‐discrete element method. International Journal for Numerical and Analytical Methods in Geomechanics, 43:1724-1743, 2019. https://doi.org/10.1002/nag.2929
Rougier, E., Knight, E.E., & Munjiza, A. Integrated solver for fluid driven fracture and fragmentation. US Patent US10275551B2, granted 30 April 2019.
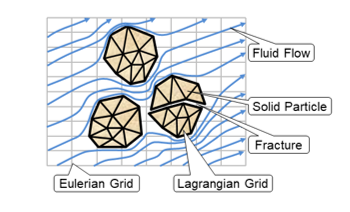

Munjiza, A., Rougier, E., Lei, Z. & Knight, E.E. 2020. FSIS – A novel Fluid-Solid Interaction Solver for Fracturing and Fragmenting Solids. Comp. Part. Mech. https://doi.org/10.1007/s40571-020-00314-9
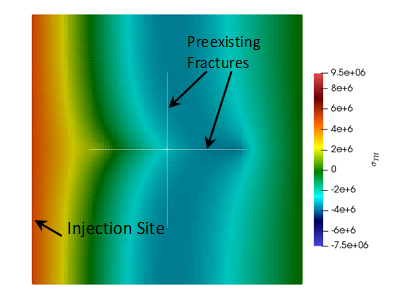
Jansen, G., Valley, B., Miller, S.A. THERMAID-A matlab package for thermo-hydraulic modeling and fracture stability analysis in fractured reservoirs. arXiv: 1806.10942.
Knight, E.E., Rougier, E., Lei, z., Euser, B., Chau, V., Boyce, S., Gao, K., Okubo, K., Froment, M. 2020. HOSS: An Implementation of the Combined Finite-Discrete Element Method. Comp. Part. Mech. https://doi.org/10.1007/s40571-020-00349-y
Utilizing a generalized massively parallel solution based on a virtual parallel machine for FDEM, it has been demonstrated that large increases to the number of processors only results in marginal increases in the specific time. This solution is problem-specific (as opposed to computer architecture specific) thus, a parallel FDEM code can be adapted to different hardware platforms ranging from desktops to 10,000+ node high-performance-computing (HPC) clusters.
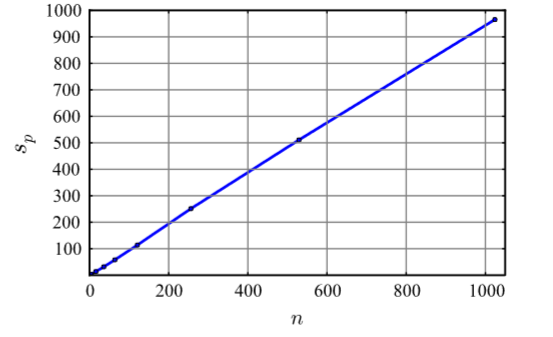
Lei, Z., Rougier, E., Knight, E.E., & Munjiza, A. 2014. A Framework for Grand Scale Parallelization of the Combined Finite Discrete Element Method in 2D. Comp. Part. Mech. 1, 307-319. https://doi.org/10.1007/s40571-014-0026-3


