17.2 ELL_Matrix Methods
The CÆSAR Code Package uses the ELL_Matrix class to contain and
manipulate algebraic matrices. The following discussion assumes that A and
B are matrices of dimension
M×N, ai, j is an element of A,
x is a vector of length N, and y is a vector of length M.
The CÆSAR Code Package contains procedures to calculate matrix norms and
matrix-vector products. In parallel, these operations require global
communication. Matrix-vector products (MatVecs) are defined by
Ax = y = 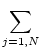 ai, j xj . ai, j xj .
|
(17.9) |
A matrix norm is any scalar-valued function on a matrix, denoted by the
double bar notation
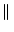 A
A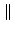 , that satisfies these properties:
, that satisfies these properties:
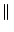 A A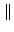 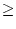 0 0 |
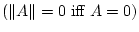 , , |
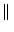 A + B A + B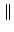 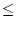 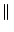 A A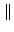 + + 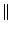 B B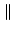 , , |
|
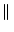 sA sA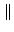 = = 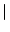 s s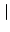 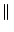 A A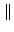 , , |
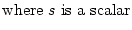 . . |
|
(17.10) |
A frequently used matrix norm is the Frobenius norm:
The general class of matrix norms known as the p-norms are defined in
terms of vector norms by:
In particular, the 1 and 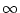 norms are the most easily calculated:
norms are the most easily calculated:
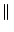 A A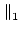 |
= |
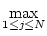 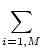 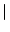 ai, j ai, j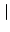 (maximum absolute column sum), (maximum absolute column sum), |
(17.13) |
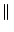 A A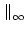 |
= |
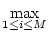 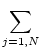 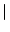 ai, j ai, j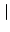 (maximum absolute row sum). (maximum absolute row sum). |
(17.14) |
In general, p-norms are difficult to calculate. The 2-norm can be
shown to be:
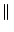 A A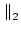 |
= |
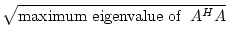 , , |
(17.15) |
| |
= |
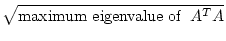 , ,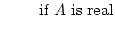 , , |
(17.16) |
where AH is the Hermitian (or complex conjugate transpose, or adjoint)
of A. Calculating the 2-norm of a matrix requires an iterative
procedure, and is not currently done in CÆSAR (only Frobenius, p = 1
and p = 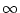 norms are calculated). However, CÆSAR calculates an
estimate of the 2-norm as a range (or the middle of the range) using the
following relationships:
norms are calculated). However, CÆSAR calculates an
estimate of the 2-norm as a range (or the middle of the range) using the
following relationships:
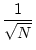 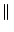 A A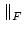 |
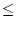 |
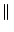 A A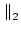 |
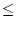 |
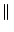 A A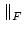 , , |
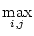 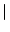 ai, j ai, j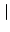 |
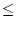 |
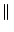 A A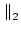 |
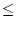 |
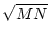 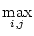 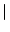 ai, j ai, j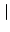 , , |
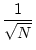 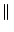 A A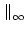 |
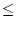 |
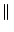 A A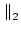 |
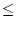 |
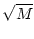 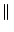 A A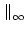 , , |
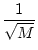 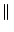 A A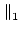 |
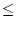 |
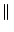 A A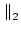 |
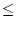 |
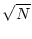 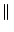 A A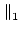 , , |
| |
|
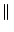 A A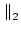 |
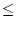 |
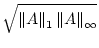 . . |
|
(17.17) |
For a similar but more complete discussion of matrix operations see
Golub & Van Loan (1989).
Michael L. Hall
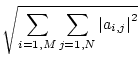 .
.
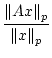 =
=