17.1 Mathematic_Vector Methods
The CÆSAR Code Package uses the Mathematic_Vector class to contain
and manipulate algebraic vectors. The following discussion assumes that
x and y are vectors of length N.
The CÆSAR Code Package contains procedures to calculate norms and
dot products of vectors. In parallel, these operations require global
communication. Dot products are defined by
xTy = x . y = 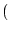 x, y x, y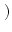 = = 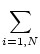 xi yi . xi yi .
|
(17.1) |
A vector norm is any scalar-valued function on a vector, denoted by the
double bar notation
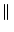 x
x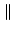 , that satisfies these properties:
, that satisfies these properties:
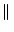 x x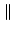 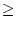 0 0 |
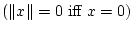 , , |
 x + y x + y 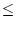 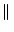 x x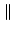 + + 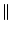 y y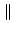 , , |
|
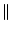 sx sx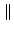 = = 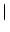 s s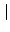 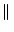 x x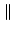 , , |
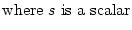 . . |
|
(17.2) |
The general class of vector norms known as the p-norms are defined by
In particular, the 1, 2, and 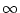 norms are the most important:
norms are the most important:
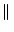 x x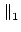 |
= |
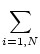  xi xi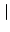 , , |
(17.4) |
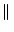 x x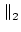 |
= |
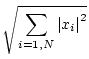 = 160#34 , and = 160#34 , and |
(17.5) |
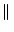 x x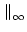 |
= |
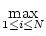 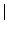 xi xi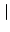 . . |
(17.6) |
The following vector norm relationships are verified by the
Mathematic_Vector Valid_State procedure:
The Cauchy-Schwartz inequality is verified by the Mathematic_Vector
DotProduct procedure:
For a similar but more complete discussion of vector operations see
Golub & Van Loan (1989).
Michael L. Hall
![$\displaystyle \sqrt[\raisebox{1ex}{$p$}]{{\sum_{i=1,N} \left\vert x_i \right\vert^p}}$](img152.gif) , p
, p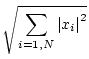 = 160#34 , and
= 160#34 , and