

Next: Properties of the Scheme
Up: Morel99b
Previous: Overview
- The purpose of this paper is to present a local support-operators diffusion discretization for arbitrary 3-D hexahedral meshes.
- We use the standard finite-element definition for hexahedra [1].
- The method that we present is a generalization of a similar scheme for 2-D r - z
quadrilateral meshes that was developed by Morel, Roberts, and Shashkov [2].
- We assume a logically-rectangular mesh in our derivation for convenience, but the scheme can also be applied to unstructured meshes.
- The diffusion equation that we seek to solve can be expressed in the following general form:
where t
denotes the time variable,
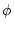 denotes a scalar
function that we refer to as the intensity, D
denotes the diffusion
coefficient, and Q
denotes the source or driving function. It is
sometimes useful to express this equation in terms of a vector function,
denotes a scalar
function that we refer to as the intensity, D
denotes the diffusion
coefficient, and Q
denotes the source or driving function. It is
sometimes useful to express this equation in terms of a vector function,
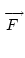 , that we refer to as the flux:
, that we refer to as the flux:


Next: Properties of the Scheme
Up: Morel99b
Previous: Overview
Michael L. Hall