

Next: Solution of the Equations
Up: Morel99a
Previous: Introduction
In this section we describe the support-operators method. It is convenient at this
point to define a flux operator given by
- D . The diffusion
operator of interest is given by the product of the divergence operator and the
flux operator:
-
. The diffusion
operator of interest is given by the product of the divergence operator and the
flux operator:
- 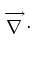 D
D . The support-operators method is based
upon the following three facts:
. The support-operators method is based
upon the following three facts:
- Given appropriately defined scalar and vector inner products, the divergence
and flux operators are adjoint to one another.
- The adjoint of an operator varies with the definition of its associated inner
products, but is unique for fixed inner products.
- The product of an operator and its adjoint is a self-adjoint positive-definite
operator.
The mathematical details relating to these facts are given in
[8]. As explained in [8], the adjoint relationship between the
flux and divergence operators is embodied in the following integral
identity:
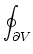 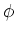 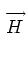 . . 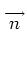 dA - dA - 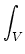 D-1 D-1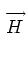 . D . D 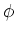 dV = dV = 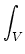 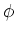 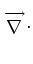 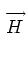 dV , dV ,
|
(4) |
where 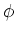 is an arbitrary scalar function,
is an arbitrary scalar function,
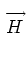 is an arbitrary vector
function, V
denotes a volume,
is an arbitrary vector
function, V
denotes a volume,
 V
denotes its surface, and
V
denotes its surface, and
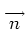 denotes the outward-directed unit normal associated with that surface.
Our support-operators method can be conceptually described in the simplest terms
as follows:
denotes the outward-directed unit normal associated with that surface.
Our support-operators method can be conceptually described in the simplest terms
as follows:
- Define discrete scalar and vector spaces to be used in a discretization of
Eq. (4).
- Fully discretize all but the flux operator in Eq. (4) over a
single arbitrary cell. The flux operator is left in the general form
of a discrete vector as defined in Step 1.
- Solve for the discrete flux operator (i.e., for its vector
components) on a single arbitrary cell by requiring that the discrete version of
Eq. (4) hold for all elements of the discrete scalar and vector spaces defined in
Step 1.
- Obtain the interior-mesh discretization of Eq. (4) by connecting adjacent mesh
cells in such a way as to ensure that Eq. (4) is satisfied over the whole grid. This
simply amounts to enforcing continuity of intensity and flux at the cell interfaces.
- Change the flux operator at those cell faces on the exterior mesh
boundary so as to satisfy the appropriate boundary conditions.
- Combine the global divergence matrix and the global flux matrix
to obtain the global diffusion matrix.
The actual method is somewhat more complicated because of the presence of both
cell-center and cell-face intensities, but this description nonetheless conveys the
central theme of the method.
To make this process concrete, we next generate the diffusion matrix for a hexahedral
mesh in Cartesian geometry. To simplify the presentation, we assume a
logically-rectangular mesh. However, our discretization scheme can be used with
unstructured meshes as well. The assumption of a logically-rectangular mesh
merely simplifies our notation and mesh indexing. Our first step is to define that
indexing. For reasons explained later, both global and local indices are used. Let
us first consider the global indices. The cell centers carry integral global
indices, e.g.,
(i, j, k)
; cell vertices carry half-integral global indices, e.g.,
(i + 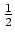 , j +
, j + 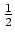 , k +
, k + 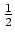 )
; and face centers carry mixed global indices composed of both
integral and half-integral indices, e.g.,
(i +
)
; and face centers carry mixed global indices composed of both
integral and half-integral indices, e.g.,
(i + 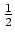 , j, k)
. The global indices for four of the vertices associated with cell
(i, j, k)
are illustrated in Fig. 1.
, j, k)
. The global indices for four of the vertices associated with cell
(i, j, k)
are illustrated in Fig. 1.
Figure 1:
Global indices for four vertices associated with cell (i, j, k)
.
|
|
Local indices allow us to uniquely define certain quantities that are associated with
a vertex or face center and a cell. For instance, the local indices for the
six faces associated with each cell are given by L, R, B, T, D, and U,
which denote Left, Right, Bottom, Top, Down, and Up respectively. This local
face indexing is illustrated for cell (i, j, k)
in Fig. 2 and Fig. 3 together with
a mapping between the local indices and the corresponding global indices.
Figure 2:
Local and global indices for three of six face centers associated
with cell (i, j, k)
.
|
|
Figure 3:
Local and global indices for three of six face centers associated
with cell (i, j, k)
.
|
|
Note that the index i
increases when moving from Left to Right, the
index j
increases when moving from Bottom to Top, and the index
k
increases when moving from the Down to Up. The local indices for
the vertices follow directly from the face indices in that each vertex is uniquely
shared by three faces of the cell. Thus the vertex shared by the Right, Top, and Up
faces is denoted by the index RTU. This vertex is illustrated in
Fig. 4.
Figure 4:
Vertex shared by the Right, Top, and Up faces having local index RTU.
|
|
The vector and matrix notation used from this point forward in this paper is
as follows. Each vector is denoted by an upper-case symbol and the components of that
vector are denoted by the corresponding lower-case symbol. An arrow is placed
over the upper-case symbol if the vector is physical, while a chevron is
placed above the upper-case symbol if the vector is algebraic. Each matrix is denoted
by a bold-face upper-case symbol and the elements of that matrix are denoted by the
corresponding lower-case symbol.
The intensities (scalars) are
defined to exist at both cell center:
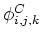 , and on the face centers:
, and on the face centers:
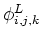 ,
,
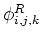 ,
,
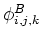 ,
,
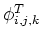 ,
,
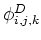 ,
,
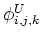 . As previously noted,
the use of local indices implies that a quantity is uniquely associated with a single
cell. For instance, unless it is otherwise stated, one should assume that
. As previously noted,
the use of local indices implies that a quantity is uniquely associated with a single
cell. For instance, unless it is otherwise stated, one should assume that
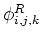
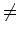
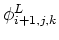 .
.
Vectors are defined in terms of face-area components located at the face
centers:
fLi, j, k
,
fRi, j, k
,
fBi, j, k
,
fTi, j, k
,
fDi, j, k
,
fUi, j, k
, where
fLi, j, k
denotes the dot product of
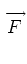 with the outward-directed area
vector located at the center of the left face of cell i, j, k
. The other face-area
components are defined analogously. The area vector is defined as the integral of the
outward-directed unit normal vector over the face, i.e.,
with the outward-directed area
vector located at the center of the left face of cell i, j, k
. The other face-area
components are defined analogously. The area vector is defined as the integral of the
outward-directed unit normal vector over the face, i.e.,
where
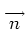 is a unit vector that is normal to the face at each point on the
face. The average outward-directed unit normal vector for the face is defined
as follows:
where
|
is a unit vector that is normal to the face at each point on the
face. The average outward-directed unit normal vector for the face is defined
as follows:
where
|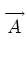 |
denotes the magnitude (standard Euclidean norm) of
|
denotes the magnitude (standard Euclidean norm) of
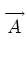 .
Equation (6) can be used to convert face-area flux components to face-normal
components if desired, e.g.
.
Equation (6) can be used to convert face-area flux components to face-normal
components if desired, e.g.
Note that
|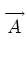 |
is equal to the face area only when the face is flat.
Interestingly, the true face areas never arise in our discretization scheme. Since it
takes three components to define a full vector, the full vectors are considered to be
located at the cell vertices:
|
is equal to the face area only when the face is flat.
Interestingly, the true face areas never arise in our discretization scheme. Since it
takes three components to define a full vector, the full vectors are considered to be
located at the cell vertices:
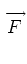 LBDi, j, k
,
LBDi, j, k
,
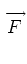 RBDi, j, k
,
RBDi, j, k
,
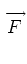 LTDi, j, k
,
LTDi, j, k
,
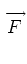 RTDi, j, k
,
RTDi, j, k
,
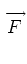 LBUi, j, k
,
LBUi, j, k
,
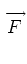 RBUi, j, k
,
RBUi, j, k
,
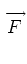 LTUi, j, k
,
LTUi, j, k
,
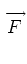 RTUi, j, k
.
Each vertex vector is constructed using the face-area components and area
vectors associated with the three faces that share that vertex. For instance,
It is convenient for our purposes to define an algebraic vector,
RTUi, j, k
.
Each vertex vector is constructed using the face-area components and area
vectors associated with the three faces that share that vertex. For instance,
It is convenient for our purposes to define an algebraic vector, 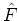 , consisting
of the three face-area components associated with the physical vector,
, consisting
of the three face-area components associated with the physical vector,
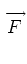 ,
e.g.,
,
e.g.,
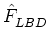 = =  fLi, j, k, fBi, j, k, fDi, j, k fLi, j, k, fBi, j, k, fDi, j, k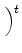 , ,
|
(9) |
where a superscript ``t'' denotes ``transpose.'' The three face-area components
associated with the Right-Top-Up vertex are illustrated in Fig. 5.
Figure 5:
Three face-center face-area components defining the flux vector at
vertex RTU.
|
|
The other vertex
vectors are defined in analogy with Eqs. (8) and (9).
As explained in Reference [8], the adjoint relationship between the gradient
and divergence operators is embodied in the following integral identity:
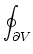  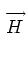 . . 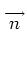 dA - dA - 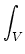 D-1 D-1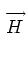 . D . D 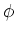 dV = dV = 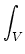 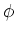 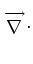 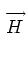 dV , dV ,
|
(10) |
where 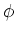 is an arbitrary scalar function,
is an arbitrary scalar function,
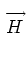 is an arbitrary vector
function, V
denotes a volume,
is an arbitrary vector
function, V
denotes a volume,
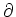 V
denotes its surface, and
V
denotes its surface, and
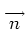 denotes the outward-directed unit normal associated with that surface. The
vector
denotes the outward-directed unit normal associated with that surface. The
vector
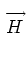 has the same mesh locations as the flux vector
has the same mesh locations as the flux vector
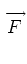 , but is not
necessarily equal to
- D
, but is not
necessarily equal to
- D
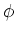 . We stress that the function
. We stress that the function
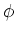 at this point represents an arbitrary scalar function, and not necessarily
the solution of the diffusion equation. The next step in our support-operators method
is to discretize Eq. (10) over a single arbitrary cell in a special manner.
Specifically, we explicitly discretize all but the flux operator, which
is expressed in an implicit form consistent with our choice of discrete
vector unknowns. We assume indices of i, j, k
for the arbitrary cell, but suppress
these indices whenever possible in the discrete approximation to
Eq. (10) that follows. We first discretize the surface integral:
at this point represents an arbitrary scalar function, and not necessarily
the solution of the diffusion equation. The next step in our support-operators method
is to discretize Eq. (10) over a single arbitrary cell in a special manner.
Specifically, we explicitly discretize all but the flux operator, which
is expressed in an implicit form consistent with our choice of discrete
vector unknowns. We assume indices of i, j, k
for the arbitrary cell, but suppress
these indices whenever possible in the discrete approximation to
Eq. (10) that follows. We first discretize the surface integral:
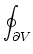 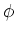 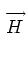 . . 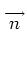 dA dA 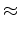 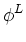 hL + hL + 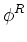 hR + hR + 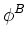 hB + hB + 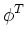 hT + hT + 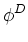 hD + hD + 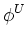 hU. hU.
|
(11) |
Next we approximate the flux volumetric integral:
D-1 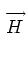 LBD . LBD . 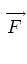 LBD LBD VLBD VLBD |
+ |
D-1 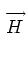 RBD . RBD . 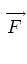 RBD RBD VRBD VRBD |
|
D-1 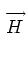 LTD . LTD . 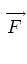 LTD LTD VLTD VLTD |
+ |
D-1 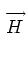 RTD . RTD . 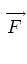 RTD RTD VRTD VRTD |
|
D-1 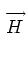 LBU . LBU . 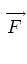 LBU LBU VLBU VLBU |
+ |
D-1 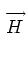 RBU . RBU . 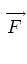 RBU RBU VRBU VRBU |
|
D-1 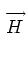 LTU . LTU . 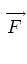 LTU LTU VLTU VLTU |
+ |
D-1 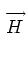 RTU . RTU . 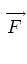 RTU RTU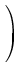 VRTU , VRTU , |
(12) |
where
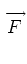 LBD
denotes
- D
LBD
denotes
- D
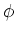 at the Left-Bottom-Down vertex, and
VLBD
denotes the volumetric weight associated with the Left-Bottom-Down vertex.
The remaining flux vectors and vertex volumetric weights are
analogously indexed. The choice of weights is one of the many free parameters in the
support-operators method. We have investigated several different choices.
Specifically:
at the Left-Bottom-Down vertex, and
VLBD
denotes the volumetric weight associated with the Left-Bottom-Down vertex.
The remaining flux vectors and vertex volumetric weights are
analogously indexed. The choice of weights is one of the many free parameters in the
support-operators method. We have investigated several different choices.
Specifically:
- Each vertex weight can be given by one-eighth the triple product
associated with the vertex. For instance, using the local vertex indexing shown in
Fig. 2, the volumetric weight for the Left-Bottom-Down vertex is given by
VLBD = 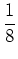  1, 2 x 1, 2 x 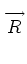 1, 3 . 1, 3 . 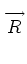 1, 4 , 1, 4 ,
|
(13) |
where
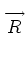 i, j
denotes the vector from vertex i
to vertex j
. Note that
these vertex weights do not sum to the total volume of the hexahedron unless the
hexahedron is a parallelepiped. We refer to these weights as the triple-product
weights.
i, j
denotes the vector from vertex i
to vertex j
. Note that
these vertex weights do not sum to the total volume of the hexahedron unless the
hexahedron is a parallelepiped. We refer to these weights as the triple-product
weights.
- The weights given in Eq. (13) can be normalized, i.e., multiplied by a
single constant, so that they sum to the exact cell volume. We refer to
these weights as the normalized triple product weights.
- Each vertex weight can be set equal to the volume of an associated
sub-hexahedron. The sub-hexahedra are obtained by using four straight lines to
connect each face center with the four edge centers adjacent to it, and by using six
straight lines to connect the cell-center with the six face centers. A
sub-hexahedron is illustrated in Fig. 6.
Figure 6:
Sub-hexahedron associated with vertex.
|
|
Although it may not be obvious, each outer
face of each sub-hexahedron coincides with a face of the hexahedron. Thus the volumes
of the sub-hexahedra always sum to the total hexahedron volume. This is perhaps the
most natural choice for the volumetric weights. We refer to these weights as the
sub-hexahedron weights.
- Each vertex weight can be set to one-eighth of the total hexahedron volume. We
refer to these weights as the one-eighth weights.
Computational testing indicates that the sub-hexahedron and one-eighth weights are
decidedly inferior to the triple-product and normalized triple-product weights.
In particular, the triple-product and normalized triple-product weights both yield a
second-order-accurate diffusion discretization, whereas the sub-hexahedron and
one-eighth weights yield a first-order accurate diffusion discretization. Although
they both give second-order accuracy, the normalized triple-product weights seem
to be slightly more accurate than the triple product weights. Thus we use the
normalized triple-product weights.
One can evaluate the dot products in Eq. (12) using Eq. (8), but we find it better
for our purposes to evaluate them with the algebraic face-area flux vectors defined
by Eq. (9). This is achieved by first transforming the face-area vectors to Cartesian
vectors and then taking the dot product. Rather than explicitly define the
matrix that transforms face-area vectors to Cartesian vectors, we explicitly define
its inverse. The desired transformation matrix can then be obtained by either
algebraic or numerical inversion. For instance, let us consider the
Left-Bottom-Down vertex vectors. We denote the matrix that transforms face-area
vectors to Cartesian vectors as ALBD
. Its inverse is the matrix that transforms
Cartesian vectors to face-area vectors:
where 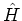 denotes a Left-Bottom-Down face-area flux vector,
and
denotes a Left-Bottom-Down face-area flux vector,
and
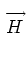 denotes a Left-Bottom-Down Cartesian flux vector,
and
where aLx
denotes the x-component of the area vector associated with the left
face. The remaining components of the matrix are defined analogously. Transforming
the face-area vector for the Left-Bottom-Down vertex, we obtain:
denotes a Left-Bottom-Down Cartesian flux vector,
and
where aLx
denotes the x-component of the area vector associated with the left
face. The remaining components of the matrix are defined analogously. Transforming
the face-area vector for the Left-Bottom-Down vertex, we obtain:
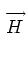 LBD . LBD . 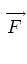 LBD LBD |
= |
A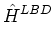 . ALBD . ALBD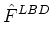 , , |
|
| |
= |
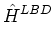 . SLBD . SLBD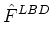 , , |
(18) |
where
Following Eq. (19), We now rewrite Eq. (12) in terms of face-area vectors as follows:
D-1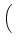 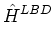 . SLBD . SLBD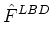  VLBD VLBD |
+ |
D-1 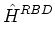 . SRBD . SRBD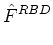 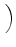 VRBD VRBD |
|
D-1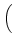 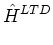 . SLTD . SLTD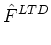 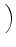 VLTD VLTD |
+ |
D-1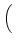 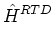 . SRTD . SRTD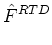  VRTD VRTD |
|
D-1 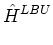 . SLBU . SLBU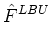  VLBU VLBU |
+ |
D-1 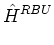 . SRBU . SRBU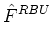 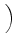 VRBU VRBU |
|
D-1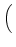 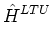 . SLTU . SLTU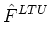 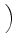 VLTU VLTU |
+ |
D-1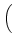 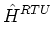 . SRTU . SRTU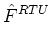  VRTU . VRTU . |
(20) |
Although we assume a single diffusion coefficient in each cell in this paper, we
note that our scheme can accommodate a different diffusion coefficient for each
vertex. In particular, Eq. (20) becomes
DLBD-1 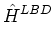 . SLBD . SLBD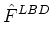 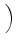 VLBD VLBD |
+ |
DRBD-1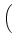 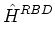 . SRBD . SRBD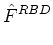 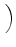 VRBD VRBD |
|
DLTD-1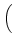 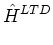 . SLTD . SLTD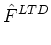 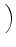 VLTD VLTD |
+ |
DRTD-1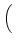 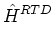 . SRTD . SRTD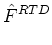  VRTD VRTD |
|
DLBU-1 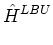 . SLBU . SLBU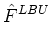 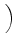 VLBU VLBU |
+ |
DRBU-1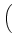 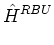 . SRBU . SRBU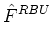  VRBU VRBU |
|
DLTU-1 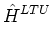 . SLTU . SLTU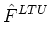 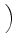 VLTU VLTU |
+ |
DRTU-1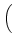 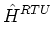 . SRTU . SRTU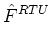  VRTU , VRTU , |
(21) |
Although we assume a scalar diffusion coefficient in this paper, we note that our
scheme can accommodate a tensor diffusion coefficient. Specifically, with a
tensor diffusion coefficient at each vertex, Eq. (21) becomes
 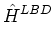 . GLBD . GLBD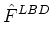  VLBD VLBD |
+ |
 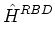 . GRBD . GRBD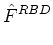  VRBD VRBD |
|
 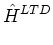 . GLTD . GLTD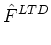 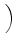 VLTD VLTD |
+ |
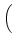 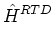 . GRTD . GRTD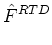  VRTD VRTD |
|
 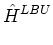 . GLBU . GLBU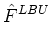 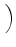 VLBU VLBU |
+ |
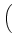 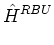 . GRBU . GRBU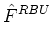  VRBU VRBU |
|
 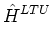 . GLTU . GLTU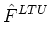 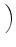 VLTU VLTU |
+ |
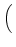 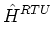 . GRTU . GRTU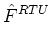  VRTU , VRTU , |
(22) |
where
and
DLBD
is the Left-Bottom-Down diffusion tensor in the Cartesian
basis. The remaining
G
-matrices are defined analogously. The diffusion
tensor must be symmetric positive-definite to ensure that its inverse exists and that
the coefficient matrix for our diffusion scheme is symmetric positive-definite.
Finally, we approximate the divergence volumetric integral:
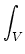 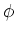 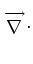 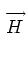 dV dV  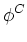  hL + hR + hB + hT + hD + hU hL + hR + hB + hT + hD + hU![$\displaystyle \left.\vphantom{ h^{L} + h^{R} +
h^{B} + h^{T} + h^{D} + h^{U} }\right]$](img139.gif) . .
|
(24) |
Equations (11), (20), and (24) are certainly not unique, but they
are fairly straightforward. For instance, Eq. (11) represents a face-centered
second-order approximation to a surface integral. Equation (20) represents a
vertex-based volumetric integral consisting of a dot-product contribution from each
pair of vertex vectors. Equation (24) is a particularly simple second-order
approximation which gives all of the weight to the cell-center value of 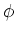 while
using a surface-integral formulation for
while
using a surface-integral formulation for
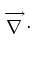
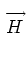 that is analogous to the
surface-integral used in Eq. (11).
that is analogous to the
surface-integral used in Eq. (11).
Substituting from Eqs. (11), (20), and
(24) into Eq. (10), we obtain the discrete version of Eq. (10):
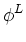 hL + hL + 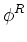 hR + hR + 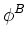 hB + hB + 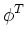 hT + hT + 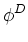 hD + hD + 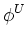 hU + hU + |
D-1 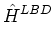 . SLBD . SLBD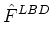  VLBD + D-1 VLBD + D-1 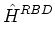 . SRBD . SRBD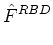  VRBD + VRBD + |
D-1 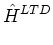 . SLTD . SLTD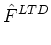 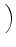 VLTD + D-1 VLTD + D-1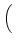 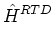 . SRTD . SRTD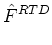  VRTD + VRTD + |
D-1 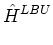 . SLBU . SLBU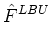 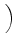 VLBU + D-1 VLBU + D-1  . SRBU . SRBU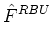  VRBU + VRBU + |
D-1 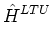 . SLTU . SLTU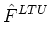  VLTU + D-1 VLTU + D-1 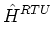 . SLTU . SLTU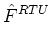  VRTU = VRTU = |
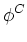  hL + hR + hB + hT + hD + hU hL + hR + hB + hT + hD + hU![$\displaystyle \left.\vphantom{ h^{L} + h^{R} +
h^{B} + h^{T} + h^{D} + h^{U} }\right]$](img139.gif) . . |
|
(25) |
Note that Eq. (25) defines the discrete inner products, discussed in Reference 8, that
are associated with the adjoint relationship between the divergence and gradient
operators. We can now use this relationship to solve for the flux
operator components by requiring that the resulting discretized identity hold
for all discrete 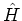 and
and 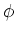 values. In particular, the equation for
the face-area component of
values. In particular, the equation for
the face-area component of
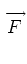 on any given cell face is obtained from
Eq. (25) simply by setting the same face-area component of
on any given cell face is obtained from
Eq. (25) simply by setting the same face-area component of
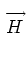 on that face to
unity and setting the remaining face-area components of
on that face to
unity and setting the remaining face-area components of
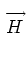 on all other faces
to zero. For instance, we obtain the equation for
fL
from Eq. (25) by setting hL
to unity and all the other face-area
components of
on all other faces
to zero. For instance, we obtain the equation for
fL
from Eq. (25) by setting hL
to unity and all the other face-area
components of
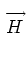 , i.e., hR
, hB
, hT
, hD
, hU
, to zero:
, i.e., hR
, hB
, hT
, hD
, hU
, to zero:
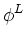 + + |
D-1 sL, LLBDfL + sL, BLBDfB + sL, DLBDfD sL, LLBDfL + sL, BLBDfB + sL, DLBDfD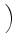 VLBD VLBD |
|
| + |
D-1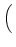 sL, LLTDfL + sL, TLTDfT + sL, DLTDfD sL, LLTDfL + sL, TLTDfT + sL, DLTDfD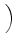 VLTD VLTD |
|
| + |
D-1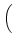 sL, LLBUfL + sL, BLBUfB + sL, ULBUfU sL, LLBUfL + sL, BLBUfB + sL, ULBUfU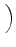 VLBU VLBU |
|
| + |
D-1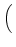 sL, LLTUfL + sL, TLTUfT + sL, ULTUfU sL, LLTUfL + sL, TLTUfT + sL, ULTUfU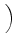 VLTU VLTU |
= 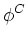 , , |
|
(26) |
where
sL, LLBD
denotes the (L, L)
element of the matrix
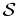 LBD
defined by Eq. (19). The remaining
S
-matrix elements are defined
analogously. We obtain the equation for fR
from Eq. (25) by setting hR
to unity
and all the other face components of
LBD
defined by Eq. (19). The remaining
S
-matrix elements are defined
analogously. We obtain the equation for fR
from Eq. (25) by setting hR
to unity
and all the other face components of
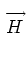 to zero:
to zero:
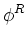 + + |
D-1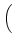 sR, RRBDfR + sR, BRBDfB + sR, DRBDfD sR, RRBDfR + sR, BRBDfB + sR, DRBDfD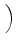 VRBD VRBD |
|
| + |
D-1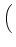 sR, RRTDfR + sR, TRTDfT + sR, DRTDfD sR, RRTDfR + sR, TRTDfT + sR, DRTDfD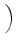 VRTD VRTD |
|
| + |
D-1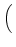 sR, RRBUfR + sR, BRBUfB + sR, URBUfU sR, RRBUfR + sR, BRBUfB + sR, URBUfU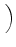 VRBU VRBU |
|
| + |
D-1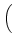 sR, RRTUfR + sR, TRTUfT + sR, URTUfU sR, RRTUfR + sR, TRTUfT + sR, URTUfU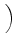 VRTU VRTU |
= 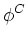 . . |
|
(27) |
We obtain the equation for fB
from Eq. (25) by setting hB
to unity and all the
other face components of
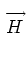 to zero:
to zero:
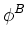 + + |
D-1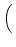 sB, LLBDfL + sB, BLBDfB + sB, DLBDfD sB, LLBDfL + sB, BLBDfB + sB, DLBDfD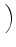 VLBD VLBD |
|
| + |
D-1 sB, RRBDfR + sB, BRBDfB + sB, DRBDfD sB, RRBDfR + sB, BRBDfB + sB, DRBDfD VRBD VRBD |
|
| + |
D-1 sB, LLBUfL + sB, BLBUfB + sB, ULBUfU sB, LLBUfL + sB, BLBUfB + sB, ULBUfU VLBU VLBU |
|
| + |
D-1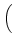 sB, RRBUfR + sB, BRBUfB + sB, URBUfU sB, RRBUfR + sB, BRBUfB + sB, URBUfU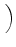 VRBU VRBU |
= 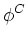 . . |
|
(28) |
We obtain the equation for fT
from Eq. (25) by setting hT
to unity and all the
other face components of
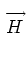 to zero:
to zero:
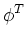 + + |
D-1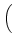 sT, LLTDfL + sT, TLTDfT + sT, DLTDfD sT, LLTDfL + sT, TLTDfT + sT, DLTDfD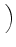 VLTD VLTD |
|
| + |
D-1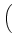 sT, RRTDfR + sT, TRTDfT + sT, DRTDfD sT, RRTDfR + sT, TRTDfT + sT, DRTDfD VRTD VRTD |
|
| + |
D-1 sT, LLTUfL + sT, TLTUfT + sT, ULTUfU sT, LLTUfL + sT, TLTUfT + sT, ULTUfU VLTU VLTU |
|
| + |
D-1 sT, RRTUfR + sT, TRTUfT + sT, URTUfU sT, RRTUfR + sT, TRTUfT + sT, URTUfU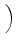 VRTU VRTU |
= 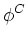 . . |
|
(29) |
We obtain the equation for fD
from Eq. (25) by setting hD
to unity and all the
other face components of
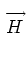 to zero:
to zero:
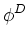 + + |
D-1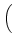 sD, LLBDfL + sD, BLBDfB + sD, DLBDfD sD, LLBDfL + sD, BLBDfB + sD, DLBDfD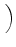 VLBD VLBD |
|
| + |
D-1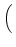 sD, RRBDfR + sD, BRBDfB + sD, DRBDfD sD, RRBDfR + sD, BRBDfB + sD, DRBDfD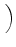 VRBD VRBD |
|
| + |
D-1 sD, LLTDfL + sD, TLTDfT + sD, DLTDfD sD, LLTDfL + sD, TLTDfT + sD, DLTDfD VLTD VLTD |
|
| + |
D-1 sD, RRTDfR + sD, TRTDfT + sD, DRTDfD sD, RRTDfR + sD, TRTDfT + sD, DRTDfD VRTD VRTD |
= 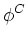 . . |
|
(30) |
Finally, we obtain the equation for fU
from Eq. (25) by setting hU
to unity and
all the other face components of
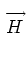 to zero:
to zero:
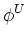 + + |
D-1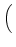 sU, LLBUfL + sU, BLBUfB + sU, ULBUfU sU, LLBUfL + sU, BLBUfB + sU, ULBUfU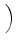 VLBU VLBU |
|
| + |
D-1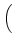 sU, RRBUfR + sU, BRBUfB + sU, URBUfU sU, RRBUfR + sU, BRBUfB + sU, URBUfU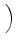 VRBU VRBU |
|
| + |
D-1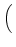 sU, LLTUfL + sU, TLTUfT + sU, ULTUfU sU, LLTUfL + sU, TLTUfT + sU, ULTUfU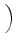 VLTU VLTU |
|
| + |
D-1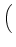 sU, RRTUfR + sU, TRTUfT + sU, URTUfU sU, RRTUfR + sU, TRTUfT + sU, URTUfU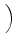 VRTU VRTU |
= 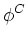 . . |
|
(31) |
Equations (26) through (31) can be expressed in matrix form as follows:
where
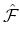 = = 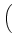 fL, fR, fB, fT, fD, fU fL, fR, fB, fT, fD, fU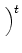 , ,
|
(33) |
and
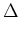 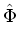 = = 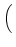 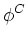 - - 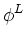 , ,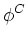 - - 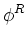 , ,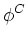 - - 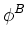 , ,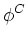 - - 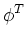 , ,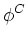 - - 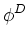 , ,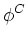 - - 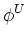 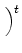 . .
|
(34) |
To obtain a matrix that gives the face-center components of the flux
operator in terms of the face-center and cell-center intensities, one need simply
invert the
6 x 6
matrix in Eq. (32):
Since it is not practical to perform this inversion algebraically, we perform it
numerically. Thus we cannot give an explicit expression for the matrix
W
. Nonetheless, it can be shown that it is an SPD
matrix (see the Appendix.) In addition, if we assume a rectangular mesh,
W
becomes diagonal and can be trivially inverted. For instance, under this
assumption, Eq. (26) becomes:
where we have also assumed that the indices i
, j
, k
, correspond to the spatial
coordinates x
, y
, z
, respectively. Solving Eq. (36) for fL
, we obtain
which is exact for 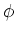 linearly-dependent upon x
.
linearly-dependent upon x
.
Having derived Eq. (35), we can construct the discrete equation for the cell-center
intensity in every cell. Each such equation represents a discretization
of Eq. (3), i.e., a balance equation for the cell. Furthermore, each
balance equation uses a discretization for the divergence of the flux that is
identical to that used in Eq. (25). In some sense, this is the point at which we
obtain a diffusion operator by combining our discrete divergence and flux operators.
Specifically, the equation for 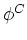 is:
is:
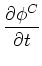 V + fL + fR + fB + fT + fD + fU = QCV , V + fL + fR + fB + fT + fD + fU = QCV ,
|
(38) |
where V
denotes the total volume of the cell, the face-area flux components are
expressed in terms of the intensities via Eq. (35), and QC
denotes the source or
driving function evaluated at cell-center. We have chosen not to discretize the time
derivative in Eq. (38) simply because essentially any standard discretization, e.g.,
the backward-Euler and Crank-Nicholson schemes [9], can be applied in
conjunction with our spatial discretization. Equation (38) contains
all of the intensities in cell (i, j, k)
. Thus it has a 7-point stencil.
Now that we have defined the equations for the cell-center intensities, we must
next define equations for the face-center intensities. Our local indexing scheme
admits two intensities and two face-area flux components at each face on the mesh
interior. In particular, there is one intensity and one flux component from each
of the cells that share a face. For instance, the cell face with
global index
(i + 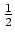 , j, k)
is associated with the two intensities,
, j, k)
is associated with the two intensities,
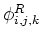 and
and
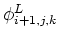 , and the two face-area flux components,
fRi, j, k
and
fLi+1, j, k
. We previously obtained the flux components in terms of the
intensities by forcing Eq. (25), a discrete version of Eq. (4), to be satisfied on each
individual cell for all discrete scalars and vectors. We now obtain equations
for the interior-mesh face-center intensities by requiring that this identity be
satisfied over the entire mesh for all discrete scalars and vectors.
, and the two face-area flux components,
fRi, j, k
and
fLi+1, j, k
. We previously obtained the flux components in terms of the
intensities by forcing Eq. (25), a discrete version of Eq. (4), to be satisfied on each
individual cell for all discrete scalars and vectors. We now obtain equations
for the interior-mesh face-center intensities by requiring that this identity be
satisfied over the entire mesh for all discrete scalars and vectors.
When Eq. (25) is summed over the entire mesh, the two volumetric integrals are
naturally approximated in terms of a sum of contributions from each individual cell.
However, a valid approximation for the the surface integral in Eq. (25) will occur if
and only if contributions to the surface integral from each individual cell cancel at
all interior faces, thereby resulting in an approximate integral over the outer
surface of the mesh. By inspection of Eq. (25) it can be seen that this will be
achieved by requiring both continuity of the intensity and continuity of the
face-area flux component at each interior cell face. In particular, we require that
|
fRi, j, k + fLi+1, j, k = 0 ,
|
(42) |
|
fTi, j, k + fBi, j+1, k = 0 ,
|
(43) |
|
fUi, j, k + fDi, j, k+1 = 0 ,
|
(44) |
where the indices in Eqs. (39) through (44) take on all values associated
with interior cell faces, and the flux components in Eqs. (42) through
(44) are expressed in terms of intensities via Eq. (35). One would expect
that the continuity of the face-area flux components expressed by Eqs. (42)
through (44) would require that the difference of the components be zero
rather than the sum of the components. However, one must remember that each of
the components is defined with respect to an area vector that is equal in magnitude
but opposite in direction to that of the other component.
Equations (39) through (41) establish that there is only one intensity
unknown associated with each interior-mesh cell face. Thus, as shown in
Eqs. (39) through (41), each such intensity can be uniquely referred to
using a global mesh index. The equations for these intensities are given by
Eqs. (42) through (44). For instance, Eq. (42) is the equation for
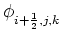 . In general, Eq. (42) contains only and all of the intensities in
cells (i, j, k)
and (i + 1, j, k)
. Thus it has a 13-point stencil. The only intensity
shared by these two cells is
. In general, Eq. (42) contains only and all of the intensities in
cells (i, j, k)
and (i + 1, j, k)
. Thus it has a 13-point stencil. The only intensity
shared by these two cells is
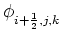 . Thus in a certain sense it can be
said that
. Thus in a certain sense it can be
said that
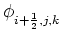 is ``chosen'' to obtain continuity of the face-area
flux components on cell-face
(i +
is ``chosen'' to obtain continuity of the face-area
flux components on cell-face
(i + 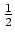 , j, k)
. The properties of Eqs. (43) and
(44) are completely analogous to those of Eq. (42).
, j, k)
. The properties of Eqs. (43) and
(44) are completely analogous to those of Eq. (42).
If the mesh is orthogonal, Eqs. (42) through (44) simplify to such an
extent that they relate each interior-mesh face-center intensity to the two
cell-center intensities adjacent to it. This enables the face-center intensities to
be explicitly eliminated, resulting in the standard 7-point cell-centered diffusion
discretization. This is completely analogous to the 2-D case discussed in detail in
[1]. However, if the mesh is non-orthogonal, the face-center intensities
cannot be eliminated, and Eqs. (42) through (44) must be included in the
diffusion matrix. In this case, these equations must be reversed in sign to
obtain a symmetric diffusion matrix:
|
- fRi, j, k - fLi+1, j, k = 0 ,
|
(45) |
|
- fTi, j, k - fBi, j+1, k = 0 ,
|
(46) |
|
- fUi, j, k - fDi, j, k+1 = 0 .
|
(47) |
Having defined the equations for the cell-center and interior-mesh face-center
intensities, we need only define the equations for the face-center intensities on the
outer mesh boundary to complete the specification of our diffusion discretization
scheme. Cell faces on the outer boundary are associated with only one cell. Thus
there is only one face-center intensity and one face-area flux component associated
with each such face. The equation for each boundary intensity is very similar to
that for each interior-mesh face-center intensity in that it expresses a continuity
of the face-normal flux component. The only difference in the boundary equations is
that the analytic boundary condition for the diffusion equation is used to define a
``ghost-cell'' face-normal flux component that must be equated to the standard
face-normal flux component defined by Eq. (35). A ghost cell is a non-existent mesh
cell that represents a continuation of the mesh across the outer mesh boundary.
For instance, assuming that the left face of cell 1, j, k
is on the outer boundary of
the mesh and its remaining faces are on the interior of the mesh, the ghost cell
``adjacent'' to cell 1, j, k
carries the indices 0, j, k
.
The analytic diffusion boundary condition of interest to us is the so-called
``extrapolated'' boundary condition. This condition is of the mixed or Robin type
and can be expressed as follows:
where de
is called the extrapolation distance, 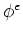 is called the extrapolated
intensity (a specified function), and
is called the extrapolated
intensity (a specified function), and
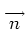 denotes an outward-directed unit
normal vector. Equation (48) is satisfied at each point on the outer surface
of the problem domain. Of course, the values of the parameters, de
and
denotes an outward-directed unit
normal vector. Equation (48) is satisfied at each point on the outer surface
of the problem domain. Of course, the values of the parameters, de
and 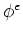 ,
may change as a function of position. One obtains a vacuum boundary condition when
,
may change as a function of position. One obtains a vacuum boundary condition when
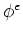 = 0
, a source condition when
= 0
, a source condition when 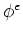 is non-zero, and a reflective
(Neumann) condition when
is non-zero, and a reflective
(Neumann) condition when
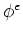 =
= 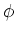 . The extrapolated boundary condition is
said to be a Marshak condition whenever de = 2D
.
. The extrapolated boundary condition is
said to be a Marshak condition whenever de = 2D
.
We begin the derivation of the ghost-cell face-area flux component by substituting
from Eq. (2) into Eq. (48):
where
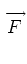 g
is the flux vector associated with a ghost cell. Next we
recognize that the outward-directed unit normal vector for a ghost-cell must be
identical to an inward-directed unit normal vector on the outer surface of the
problem domain. Thus
g
is the flux vector associated with a ghost cell. Next we
recognize that the outward-directed unit normal vector for a ghost-cell must be
identical to an inward-directed unit normal vector on the outer surface of the
problem domain. Thus
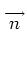 g = - g = - 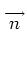 , ,
|
(50) |
where
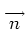 g
denotes a ghost-cell outward-directed unit normal vector.
Substituting from Eq. (50) into Eq. (49), we obtain:
Next we solve Eq. (51) for the outward-directed flux component associated with a
ghost cell:
Now let us assume that the left face of cell 1, j, k
is on the outer
boundary of the mesh with its remaining faces on the mesh interior. The ghost cell
whose right face is identical to the left face of cell 1, j, k
carries the
indices 0, j, k
. The intensity on the left face of cell (1, j, k)
is
g
denotes a ghost-cell outward-directed unit normal vector.
Substituting from Eq. (50) into Eq. (49), we obtain:
Next we solve Eq. (51) for the outward-directed flux component associated with a
ghost cell:
Now let us assume that the left face of cell 1, j, k
is on the outer
boundary of the mesh with its remaining faces on the mesh interior. The ghost cell
whose right face is identical to the left face of cell 1, j, k
carries the
indices 0, j, k
. The intensity on the left face of cell (1, j, k)
is
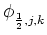 and the face-area flux component on that face is
fL1, j, k
.
Evaluating Eq. (52) at the center of face
(
and the face-area flux component on that face is
fL1, j, k
.
Evaluating Eq. (52) at the center of face
(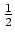 , j, k)
and multiplying the resulting
expression by the magnitude of the outward-directed area-vector on that face
associated with cell 1, j, k
, we obtain the desired expression for the ghost-cell
face-area flux component:
, j, k)
and multiplying the resulting
expression by the magnitude of the outward-directed area-vector on that face
associated with cell 1, j, k
, we obtain the desired expression for the ghost-cell
face-area flux component:
fR0, j, k = - 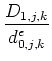 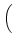 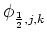 - - 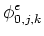  | |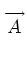 L1, j, k| , L1, j, k| ,
|
(53) |
where the extrapolated intensity and the extrapolation distance are assumed to carry
the ghost-cell index.
We next obtain the equation for
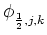 by
requiring that the Right and Left face-area flux components for cells (0, j, k)
and
(1, j, k)
, respectively, sum to zero:
by
requiring that the Right and Left face-area flux components for cells (0, j, k)
and
(1, j, k)
, respectively, sum to zero:
|
- fR0, j, k - fL1, j, k = 0 .
|
(54) |
Note that Eq. (54) is identical to Eq. (45) with the latter equation evaluated at
i = 0
. Thus Eqs. (45) through (47) provide all face-center
intensity equations with the caveat that when an intensity is on the outer mesh
boundary, the associated ghost-cell flux component must be defined via the boundary
condition rather than Eq. (35). Note that Eq. (54) couples all of the intensities
within a cell and therefore has a 7-point stencil. This completes the specification
of our diffusion discretization scheme.
To summarize,
- The face-area flux components for each cell are
expressed in terms of the intensities within that cell via Eq. (35).
- The discrete equation for each cell-centered intensity is given in
Eq. (38).
- The equations for the interior-mesh face-centered intensities are
given in Eqs. (45) through (47).
- The equation for a face-center intensity on the outer mesh boundary is given by
Eqs. (53) and (54) when the boundary face is the Left face of a cell.
Analogous equations for the other five cases are easily derived using Eqs. (45)
through (47) and Eq. (53).
It is interesting to note that the equation for a cell-center intensity contains a
time-derivative of that intensity, but the equations for the face-center equations do
not contain any form of time derivative. Thus in time-dependent calculations, one
must have initial values for the cell-center intensities, but initial values are not
required for the face-center intensities. Thus only cell-center intensities must be
saved from one time step to the next.
We have already shown that our diffusion matrix is sparse. It is also symmetric
positive-definite. We demonstrate this latter property in the Appendix.


Next: Solution of the Equations
Up: Morel99a
Previous: Introduction
Michael L. Hall
![]() . The diffusion
operator of interest is given by the product of the divergence operator and the
flux operator:
-
. The diffusion
operator of interest is given by the product of the divergence operator and the
flux operator:
- ![]() D
D![]() . The support-operators method is based
upon the following three facts:
. The support-operators method is based
upon the following three facts:
![]() , j +
, j + ![]() , k +
, k + ![]() )
; and face centers carry mixed global indices composed of both
integral and half-integral indices, e.g.,
(i +
)
; and face centers carry mixed global indices composed of both
integral and half-integral indices, e.g.,
(i + ![]() , j, k)
. The global indices for four of the vertices associated with cell
(i, j, k)
are illustrated in Fig. 1.
, j, k)
. The global indices for four of the vertices associated with cell
(i, j, k)
are illustrated in Fig. 1.
![]() , and on the face centers:
, and on the face centers:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() . As previously noted,
the use of local indices implies that a quantity is uniquely associated with a single
cell. For instance, unless it is otherwise stated, one should assume that
. As previously noted,
the use of local indices implies that a quantity is uniquely associated with a single
cell. For instance, unless it is otherwise stated, one should assume that
![]()
![]()
![]() .
.
![]() with the outward-directed area
vector located at the center of the left face of cell i, j, k
. The other face-area
components are defined analogously. The area vector is defined as the integral of the
outward-directed unit normal vector over the face, i.e.,
with the outward-directed area
vector located at the center of the left face of cell i, j, k
. The other face-area
components are defined analogously. The area vector is defined as the integral of the
outward-directed unit normal vector over the face, i.e.,
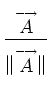 ,
,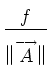 .
.![]() while
using a surface-integral formulation for
while
using a surface-integral formulation for
![]()
![]() that is analogous to the
surface-integral used in Eq. (11).
that is analogous to the
surface-integral used in Eq. (11).
![]() and
and ![]() values. In particular, the equation for
the face-area component of
values. In particular, the equation for
the face-area component of
![]() on any given cell face is obtained from
Eq. (25) simply by setting the same face-area component of
on any given cell face is obtained from
Eq. (25) simply by setting the same face-area component of
![]() on that face to
unity and setting the remaining face-area components of
on that face to
unity and setting the remaining face-area components of
![]() on all other faces
to zero. For instance, we obtain the equation for
fL
from Eq. (25) by setting hL
to unity and all the other face-area
components of
on all other faces
to zero. For instance, we obtain the equation for
fL
from Eq. (25) by setting hL
to unity and all the other face-area
components of
![]() , i.e., hR
, hB
, hT
, hD
, hU
, to zero:
, i.e., hR
, hB
, hT
, hD
, hU
, to zero:
![]() is:
is:
![]() , j, k)
is associated with the two intensities,
, j, k)
is associated with the two intensities,
![]() and
and
![]() , and the two face-area flux components,
fRi, j, k
and
fLi+1, j, k
. We previously obtained the flux components in terms of the
intensities by forcing Eq. (25), a discrete version of Eq. (4), to be satisfied on each
individual cell for all discrete scalars and vectors. We now obtain equations
for the interior-mesh face-center intensities by requiring that this identity be
satisfied over the entire mesh for all discrete scalars and vectors.
, and the two face-area flux components,
fRi, j, k
and
fLi+1, j, k
. We previously obtained the flux components in terms of the
intensities by forcing Eq. (25), a discrete version of Eq. (4), to be satisfied on each
individual cell for all discrete scalars and vectors. We now obtain equations
for the interior-mesh face-center intensities by requiring that this identity be
satisfied over the entire mesh for all discrete scalars and vectors.
![]() . In general, Eq. (42) contains only and all of the intensities in
cells (i, j, k)
and (i + 1, j, k)
. Thus it has a 13-point stencil. The only intensity
shared by these two cells is
. In general, Eq. (42) contains only and all of the intensities in
cells (i, j, k)
and (i + 1, j, k)
. Thus it has a 13-point stencil. The only intensity
shared by these two cells is
![]() . Thus in a certain sense it can be
said that
. Thus in a certain sense it can be
said that
![]() is ``chosen'' to obtain continuity of the face-area
flux components on cell-face
(i +
is ``chosen'' to obtain continuity of the face-area
flux components on cell-face
(i + ![]() , j, k)
. The properties of Eqs. (43) and
(44) are completely analogous to those of Eq. (42).
, j, k)
. The properties of Eqs. (43) and
(44) are completely analogous to those of Eq. (42).
![]() by
requiring that the Right and Left face-area flux components for cells (0, j, k)
and
(1, j, k)
, respectively, sum to zero:
by
requiring that the Right and Left face-area flux components for cells (0, j, k)
and
(1, j, k)
, respectively, sum to zero: