

Next: Second-Order Demonstration
Up: Hexahedral Support Operator Method
Previous: Support Operator Method Derivation:
The matrix
S
is symmetric, since
| ST |
= |
 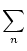 D-1nVnPTnJn-1J-TnPn D-1nVnPTnJn-1J-TnPn![$\displaystyle \left.\vphantom{ \sum_n D^{-1}_n V_n {\mathbf{P}}^{\mathrm{T}}_n
...
...n^{-1} {\mathbf{J}}^{-\mathrm{T}}_n
\mathbf{P}_n }\right]^{{{\mathrm{T}}}}_{{}}$](img108.gif) |
|
| |
= |
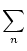 D-1nVn D-1nVn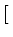 PTnJn-1J-TnPn PTnJn-1J-TnPn![$\displaystyle \left.\vphantom{ {\mathbf{P}}^{\mathrm{T}}_n
\mathbf{J}_n^{-1} {\mathbf{J}}^{-\mathrm{T}}_n
\mathbf{P}_n }\right]^{{{\mathrm{T}}}}_{{}}$](img110.gif) |
|
| |
= |
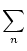 D-1nVn D-1nVn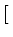 J-TnPn J-TnPn![$\displaystyle \left.\vphantom{ {\mathbf{J}}^{-\mathrm{T}}_n
\mathbf{P}_n }\right]^{{{\mathrm{T}}}}_{{}}$](img112.gif) 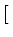 PTnJn-1 PTnJn-1![$\displaystyle \left.\vphantom{ {\mathbf{P}}^{\mathrm{T}}_n
\mathbf{J}_n^{-1} }\right]^{{{\mathrm{T}}}}_{{}}$](img114.gif) |
|
| |
= |
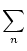 D-1nVnPnTJn-1J-TnPn D-1nVnPnTJn-1J-TnPn |
|
| |
= |
S |
|
The matrix
S
is positive definite, since
| xTSx |
= |
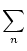 D-1nVnxTPTnJn-1J-TnPnx D-1nVnxTPTnJn-1J-TnPnx |
|
| |
= |
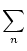 D-1nVn D-1nVn J-TnPnx J-TnPnx![$\displaystyle \left.\vphantom{
{\mathbf{J}}^{-\mathrm{T}}_n \mathbf{P}_n \mathbf{x} }\right]^{{{\mathrm{T}}}}_{{}}$](img116.gif) 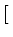 J-TnPnx J-TnPnx![$\displaystyle \left.\vphantom{ {\mathbf{J}}^{-\mathrm{T}}_n \mathbf{P}_n \mathbf{x} }\right]$](img117.gif) |
|
| |
= |
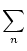 D-1nVn D-1nVn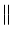 J-TnPnx J-TnPnx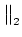 |
|
| |
> |
0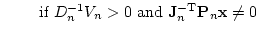 |
|
If
S
is SPD, then
S-1
is also symmetric positive definite.
This is necessary, but not sufficient, to proving that the entire method is SPD.
See the associated paper for the gory details.


Next: Second-Order Demonstration
Up: Hexahedral Support Operator Method
Previous: Support Operator Method Derivation:
Michael L. Hall