Support Operator Method Derivation: Main Derivation

Starting with a vector identity,

$$\mbox{$\mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{\nabla}$} \cdot$}$$$$\left(\vphantom{ \phi \mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{W}$} }\right.$$$$\phi$$$$\mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{W}$}$$$$\left.\vphantom{ \phi \mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{W}$} }\right)$$ = $$\phi$$$$\mbox{$\mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{\nabla}$} \cdot$}$$$$\mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{W}$}$$ + $$\mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{W}$}$$ ^. $$\mbox{$\mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{\nabla}$}$}$$$$\phi$$  ,

where $\phi$ is the scalar variable to be diffused and $\mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{W}$}$ is an arbitrary vector, integrate over a cell volume:

$$\int_{c}^{}$$$$\mbox{$\mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{\nabla}$} \cdot$}$$$$\left(\vphantom{ \phi \mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{W}$} }\right.$$$$\phi$$$$\mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{W}$}$$$$\left.\vphantom{ \phi \mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{W}$} }\right)$$ dV = $$\int_{c}^{}$$$$\phi$$$$\mbox{$\mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{\nabla}$} \cdot$}$$$$\mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{W}$}$$ dV + $$\int_{c}^{}$$$$\mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{W}$}$$ ^. $$\mbox{$\mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{\nabla}$}$}$$$$\phi$$ dV  .

Each colored term in the equation above will be treated separately.

Aside: note that, if inner products for scalars and vectors are defined by

$$\Bigg\langle$$a, b$$\Bigg\rangle$$ = $$\int_{c}^{}$$ab dV  and  $$\left\langle\vphantom{ \mbox{$\stackrel{^{\mat... ...}$},\mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{B}$} }\right.$$$$\mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{A}$}$$,$$\mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{B}$}$$$$\left.\vphantom{ \mbox{$\stackrel{^{\mathstrut... ...box{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{B}$} }\right\rangle$$ = $$\int_{c}^{}$$$$\mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{A}$}$$ ^. $$\mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{B}$}$$ dV  ,

and if $\phi$ = 0 on the boundary, such that the Green term vanishes, then this equation becomes the definition of an adjoint,

$$\left\langle\vphantom{ -\mbox{$\mbox{$\stackrel... ...box{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{W}$}, \phi }\right.$$ - $$\mbox{$\mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{\nabla}$} \cdot$}$$$$\mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{W}$}$$,$$\phi$$$$\left.\vphantom{ -\mbox{$\mbox{$\stackrel{^{\ma... ...stackrel{^{\mathstrut}\smash{\longrightarrow}}{W}$}, \phi }\right\rangle$$ = $$\left\langle\vphantom{ \mbox{$\stackrel{^{\mat... ...\stackrel{^{\mathstrut}\smash{\longrightarrow}}{\nabla}$}$}\phi }\right.$$$$\mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{W}$}$$,$$\mbox{$\mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{\nabla}$}$}$$$$\phi$$$$\left.\vphantom{ \mbox{$\stackrel{^{\mathstrut... ...rel{^{\mathstrut}\smash{\longrightarrow}}{\nabla}$}$}\phi }\right\rangle$$  ,

which shows that the divergence is the negative adjoint of the gradient. The Green term can be transformed via Gauss's Theorem into a surface integral,

$$\int_{c}^{}$$$$\mbox{$\mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{\nabla}$} \cdot$}$$$$\left(\vphantom{ \phi \mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{W}$} }\right.$$$$\phi$$$$\mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{W}$}$$$$\left.\vphantom{ \phi \mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{W}$} }\right)$$ dV = $$\oint_{S}^{}$$$$\left(\vphantom{ \phi \mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{W}$} }\right.$$$$\phi$$$$\mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{W}$}$$$$\left.\vphantom{ \phi \mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{W}$} }\right)$$ ^.  $$\mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{dA}$}$$  .

This is discretized into values defined on each face of the hexahedral cell,

$$\oint_{S}^{}$$$$\left(\vphantom{ \phi \mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{W}$} }\right.$$$$\phi$$$$\mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{W}$}$$$$\left.\vphantom{ \phi \mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{W}$} }\right)$$ ^.  $$\mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{dA}$}$$ $$\approx$$ $$\sum_{f}^{}$$$$\phi_{f}^{}$$$$\mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{W_f}$}$$ ^. $$\mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{A_f}$}$$  .

The summation over faces ($\sum_{f}^{}$ ) includes six faces (+ k , - k , + l , - l , + m , - m ), shown here for the intensity variable $\phi$ :

The Red term is approximated by first assuming that $\phi$ is constant over the cell (at the center value), and then performing a discretization similar to the previous one for the Green term:

$$\int_{c}^{} \phi \mbox{$\mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{\nabla}$} \cdot$} \mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{W}$} \approx \phi_{c}^{} \int_{c}^{} \mbox{$\mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{\nabla}$} \cdot$} \mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{W}$}$$

$$\phi_{c}^{} \oint_{S}^{} \mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{W}$} \mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{dA}$}$$ =

$$\approx \phi_{c}^{} \sum_{f}^{} \mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{W_f}$} \mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{A_f}$}$$

Turning to the final Blue term, insert the definition of the flux^3.1,

$$\mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{F}$}$$ = - D$$\mbox{$\mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{\nabla}$}$}$$$$\phi$$  ,

to get

$$\int_{c}^{}$$$$\mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{W}$}$$ ^. $$\mbox{$\mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{\nabla}$}$}$$$$\phi$$ dV = - $$\int_{c}^{}$$D^-1$$\mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{W}$}$$ ^. $$\mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{F}$}$$ dV  .

Note that by defining the flux in terms of the remainder of the equation, the gradient is being defined in terms of the divergence.

The Blue term is discretized by evaluating the integrand at each of the cell nodes (octants in 3-D) and summing:

- $$\int_{c}^{}$$D^-1$$\mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{W}$}$$ ^. $$\mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{F}$}$$ dV $$\approx$$ - $$\sum_{n}^{}$$D^-1_n$$\mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{W_n}$}$$ ^. $$\mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{F_n}$}$$V_n  .

Combining all of the discretized terms of the colored equation and changing to a linear algebra representation gives

$$\sum_{f}^{}$$$$\phi_{f}^{}$$W^T_fA_f = $$\phi_{c}^{}$$$$\sum_{f}^{}$$W^T_fA_f - $$\sum_{n}^{}$$D^-1_nW^T_nF_nV_n  .

Rearranging terms gives

$$\sum_{n}^{}$$D^-1_nW^T_nF_nV_n = $$\sum_{f}^{}$$$$\left(\vphantom{ \phi_c - \phi_f }\right.$$$$\phi_{c}^{}$$ - $$\phi_{f}^{}$$$$\left.\vphantom{ \phi_c - \phi_f }\right)$$W^T_fA_f  .

Note that the right hand side is a sum over the six faces, but the left hand side is a sum over the eight nodes.

In order to express the node-centered vectors, W_n and F_n , in terms of their face-centered counterparts, define

J^T_nW_n $$\equiv$$ $$\left[\vphantom{ \begin{array}{c} {\mathbf{W}}^{\mathrm{T}}_{f1... ...\\ [1em] {\mathbf{W}}^{\mathrm{T}}_{f3} \mathbf{A}_{f3} \end{array} }\right.$$$$\begin{array}{c} {\mathbf{W}}^{\mathrm{T}}_{f1} \mathbf{A}_{f1} \... ...{A}_{f2} \\ [1em] {\mathbf{W}}^{\mathrm{T}}_{f3} \mathbf{A}_{f3} \end{array}$$$$\left.\vphantom{ \begin{array}{c} {\mathbf{W}}^{\mathrm{T}}_{f1... ...\\ [1em] {\mathbf{W}}^{\mathrm{T}}_{f3} \mathbf{A}_{f3} \end{array} }\right]$$  ,

where f1 , f2 , and f3 are the faces adjacent to node n and the Jacobian matrix is the square matrix given by

J_n = $$\left[\vphantom{ \begin{array}{ccc} \mathbf{A}_{f1} & \mathbf{A}_{f2} & \mathbf{A}_{f3} \end{array} }\right.$$$$\begin{array}{ccc} \mathbf{A}_{f1} & \mathbf{A}_{f2} & \mathbf{A}_{f3} \end{array}$$$$\left.\vphantom{ \begin{array}{ccc} \mathbf{A}_{f1} & \mathbf{A}_{f2} & \mathbf{A}_{f3} \end{array} }\right]$$  .

Using this definition for the node-centered vectors W_n and F_n and performing some algebraic manipulations results in

$$\sum_{n}^{}$$D^-1_nV_n$$\left[\vphantom{ \begin{array}{c} {\mathbf{W}}^{\mathrm{T}}_{f1... ...\\ [1em] {\mathbf{W}}^{\mathrm{T}}_{f3} \mathbf{A}_{f3} \end{array} }\right.$$$$\begin{array}{c} {\mathbf{W}}^{\mathrm{T}}_{f1} \mathbf{A}_{f1} \... ...{A}_{f2} \\ [1em] {\mathbf{W}}^{\mathrm{T}}_{f3} \mathbf{A}_{f3} \end{array}$$$$\left.\vphantom{ \begin{array}{c} {\mathbf{W}}^{\mathrm{T}}_{f1}... ...}^{\mathrm{T}}_{f3} \mathbf{A}_{f3} \end{array} }\right]^{{{\mathrm{T}}}}_{{}}$$J_n^-1J^-T_n$$\left[\vphantom{ \begin{array}{c} {\mathbf{F}}^{\mathrm{T}}_{f1}... ...\\ [1em] {\mathbf{F}}^{\mathrm{T}}_{f3} \mathbf{A}_{f3} \end{array} }\right.$$$$\begin{array}{c} {\mathbf{F}}^{\mathrm{T}}_{f1} \mathbf{A}_{f1} ... ...{A}_{f2} \\ [1em] {\mathbf{F}}^{\mathrm{T}}_{f3} \mathbf{A}_{f3} \end{array}$$$$\left.\vphantom{ \begin{array}{c} {\mathbf{F}}^{\mathrm{T}}_{f1}... ...\\ [1em] {\mathbf{F}}^{\mathrm{T}}_{f3} \mathbf{A}_{f3} \end{array} }\right]$$ = $$\widetilde{{\mathbf{W}}}^{{{\mathrm{T}}}}_{{}}$$$$\widetilde{{\mathbf{\Phi}}}$$  .

where the sum over faces has been written as a dot product of $\widetilde{{\mathbf{W}}}$ and $\widetilde{{\mathbf{\Phi}}}$ , which are defined by

$$\widetilde{{\mathbf{W}}}$$ = $$\left[\vphantom{ \begin{array}{c} {\mathbf{W}}^{\mathrm{T}}_1 \m... ...] {\mathbf{W}}^{\mathrm{T}}_{N_{lf}} \mathbf{A}_{N_{lf}} \end{array} }\right.$$$$\begin{array}{c} {\mathbf{W}}^{\mathrm{T}}_1 \mathbf{A}_1 \\ [1... ... \\ [1em] {\mathbf{W}}^{\mathrm{T}}_{N_{lf}} \mathbf{A}_{N_{lf}} \end{array}$$$$\left.\vphantom{ \begin{array}{c} {\mathbf{W}}^{\mathrm{T}}_1 \m... ...] {\mathbf{W}}^{\mathrm{T}}_{N_{lf}} \mathbf{A}_{N_{lf}} \end{array} }\right]$$  ,      $$\widetilde{{\mathbf{\Phi}}}$$ = $$\left[\vphantom{ \begin{array}{c} \left( \phi_c - \phi_1 \right)... ... \vdots \\ [1em] \left( \phi_c - \phi_{N_{lf}} \right) \end{array} }\right.$$$$\begin{array}{c} \left( \phi_c - \phi_1 \right) \\ [1em] \left... ...\\ [1em] \vdots \\ [1em] \left( \phi_c - \phi_{N_{lf}} \right) \end{array}$$$$\left.\vphantom{ \begin{array}{c} \left( \phi_c - \phi_1 \right)... ... \vdots \\ [1em] \left( \phi_c - \phi_{N_{lf}} \right) \end{array} }\right]$$  .

N_lf is the total number of local faces, which is equal to 6 in 3-D.

To convert the short vectors involving the faces adjacent to a particular node into sparse long vectors involving all of the faces of the cell, define permutation matrices for each node, P_n , such that

$$\left[\vphantom{ \begin{array}{c} {\mathbf{W}}^{\mathrm{T}}_{f1... ...\\ [1em] {\mathbf{W}}^{\mathrm{T}}_{f3} \mathbf{A}_{f3} \end{array} }\right.$$$$\begin{array}{c} {\mathbf{W}}^{\mathrm{T}}_{f1} \mathbf{A}_{f1} \... ...{A}_{f2} \\ [1em] {\mathbf{W}}^{\mathrm{T}}_{f3} \mathbf{A}_{f3} \end{array}$$$$\left.\vphantom{ \begin{array}{c} {\mathbf{W}}^{\mathrm{T}}_{f1... ...\\ [1em] {\mathbf{W}}^{\mathrm{T}}_{f3} \mathbf{A}_{f3} \end{array} }\right]$$ = P_n$$\widetilde{{\mathbf{W}}}$$  ,

where, for example,

P_n = $$\left[\vphantom{ \begin{array}{cccccc} 0 & 0 & 1 & 0 & 0 & 0 \\ ... ... 0 & 0 & 0 & 0 & 1 & 0 \\ [1em] 0 & 1 & 0 & 0 & 0 & 0 \end{array} }\right.$$$$\begin{array}{cccccc} 0 & 0 & 1 & 0 & 0 & 0 \\ [1em] 0 & 0 & 0 & 0 & 1 & 0 \\ [1em] 0 & 1 & 0 & 0 & 0 & 0 \end{array}$$$$\left.\vphantom{ \begin{array}{cccccc} 0 & 0 & 1 & 0 & 0 & 0 \\ ... ... 0 & 0 & 0 & 0 & 1 & 0 \\ [1em] 0 & 1 & 0 & 0 & 0 & 0 \end{array} }\right]$$$$\mbox{\hspace{2em} \begin{tabular}{l} if $f1\left( n \right) = 3... ... $f2\left( n \right) = 5$, \\ and $f3\left( n \right) = 2$. \end{tabular}}$$

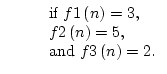
Note that P_n is rectangular, with a size of N_d x N_lf ( 3 x 6 for 3-D, 2 x 4 for 2-D, 1 x 2 for 1-D).

Using the permutation matrices, and defining $\widetilde{{\mathbf{F}}}$ in a fashion similar to $\widetilde{{\mathbf{W}}}$ ( $\widetilde{{\mathbf{F}}}$ is a vector of F^T_fA_f for each cell face), gives

$$\sum_{n}^{}$$D^-1_nV_n$$\widetilde{{\mathbf{W}}}^{{{\mathrm{T}}}}_{{}}$$P^T_nJ_n^-1J^-T_nP_n$$\widetilde{{\mathbf{F}}}$$ = $$\widetilde{{\mathbf{W}}}^{{{\mathrm{T}}}}_{{}}$$$$\widetilde{{\mathbf{\Phi}}}$$  ,

or

$$\widetilde{{\mathbf{W}}}^{{{\mathrm{T}}}}_{{}}$$$$\left[\vphantom{ \sum_n D^{-1}_n V_n {\mathbf{P}}^{\mathrm{T}}_n \mathbf{J}_n^{-1} {\mathbf{J}}^{-\mathrm{T}}_n \mathbf{P}_n }\right.$$$$\sum_{n}^{}$$D^-1_nV_nP^T_nJ_n^-1J^-T_nP_n$$\left.\vphantom{ \sum_n D^{-1}_n V_n {\mathbf{P}}^{\mathrm{T}}_n \mathbf{J}_n^{-1} {\mathbf{J}}^{-\mathrm{T}}_n \mathbf{P}_n }\right]$$$$\widetilde{{\mathbf{F}}}$$ = $$\widetilde{{\mathbf{W}}}^{{{\mathrm{T}}}}_{{}}$$$$\widetilde{{\mathbf{\Phi}}}$$  ,

or

$$\widetilde{{\mathbf{W}}}^{{{\mathrm{T}}}}_{{}}$$S$$\widetilde{{\mathbf{F}}}$$ = $$\widetilde{{\mathbf{W}}}^{{{\mathrm{T}}}}_{{}}$$$$\widetilde{{\mathbf{\Phi}}}$$  ,

where

S = $$\sum_{n}^{}$$D^-1_nV_nP^T_nJ_n^-1J^-T_nP_n  .

The original vector $\mbox{$\stackrel{^{\mathstrut}\smash{\longrightarrow}}{W}$}$ (on which W_f and $\widetilde{{\mathbf{W}}}$ are based) was an arbitrary vector. It can now be eliminated from the equation to give

S$$\widetilde{{\mathbf{F}}}$$ = $$\widetilde{{\mathbf{\Phi}}}$$  ,

which can easily be inverted to give the fluxes (dotted into the areas) in terms of the $\phi$ -differences, $\widetilde{{\mathbf{F}}}$ = S^-1$\widetilde{{\mathbf{\Phi}}}$ . This is exactly the form needed for discretization of the diffusion term within Augustus.