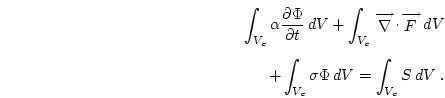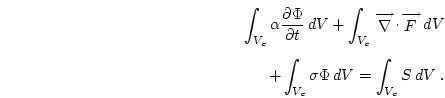Next: Flux Terms
Up: Method Derivation
Previous: Method Derivation
The first step in the derivation of the method is the discretization of
the conservation equation, Equation 2. Integrating the conservation
equation over the cell volume gives
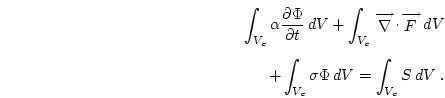
Defining cell averages and applying Gauss' Theorem gives
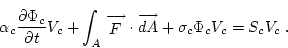
Discretizing temporally and evaluating the flux integral gives
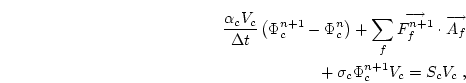
where the sum over f represents the sum over the face values, the
subscript c represents a cell-centered or cell-average value and the
unsuperscripted variables are evaluated at
n + 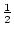 . Note that all of the
geometries in Table 1 can be represented by this equation when the
proper definitions for areas, volumes, and face sums are substituted.
Note that this scheme is not limited to fully implicit differencing; for
instance, a Crank-Nicholson differencing scheme may be employed.
. Note that all of the
geometries in Table 1 can be represented by this equation when the
proper definitions for areas, volumes, and face sums are substituted.
Note that this scheme is not limited to fully implicit differencing; for
instance, a Crank-Nicholson differencing scheme may be employed.



Next: Flux Terms
Up: Method Derivation
Previous: Method Derivation
Michael L. Hall