Second-Order Demonstration

In order to demonstrate that the method is second-order accurate, a problem with an analytic quartic³ solution is solved. The problem which is chosen is described in detail in ##more92 (##more92). The problem domain is a cube, with a random mesh obtained by moving (in 3-D) the interior points of an orthogonal mesh by a random fraction of 20 of the inter-nodal distance, in a random direction. There are reflective boundaries on four sides, and vacuum boundaries on two opposite sides. The properties are constant spatially and temporally, and there is a spatially-varying source which is proportional to x² in each cell. 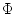With these conditions, the steady-state analytic answer is a quartic of the form 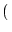$\Phi$$\left(\vphantom{ x,y,z 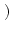}\right.$x, y, z$\left.\vphantom{ x,y,z }\right)$ = a + bx + cx⁴.

New Method

Table 2: Results from the Second-Order Accuracy Test.

Problem Size (cells)	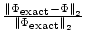${\frac{{\left\Vert \Phi_{\mbox{\scriptsize exact}} - \Phi \right\Vert _2}}{{\left\Vert \Phi_{\mbox{\scriptsize exact}} \right\Vert _2}}}$	Error Ratio
5×5×5	1.0248 ×10-2
10×10×10	2.6190 ×10-3	3.91
20×20×20	6.6082 ×10-4	3.96
40×40×40	1.6530 ×10-4	4.00

Orthogonal Seven-Point Solution

Problem Size (cells)	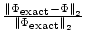${\frac{{\left\Vert \Phi_{\mbox{\scriptsize exact}} - \Phi \right\Vert _2}}{{\left\Vert \Phi_{\mbox{\scriptsize exact}} \right\Vert _2}}}$	Error Ratio
5×5×5	1.0202 ×10-2
10×10×10	2.6205 ×10-3	3.92
20×20×20	6.5952 ×10-4	3.97
40×40×40	1.6515 ×10-4	3.99

The results from running this problem for different mesh sizes are given in Table 2. It can be seen that the error is reduced by a factor of four each time the mesh spacing is reduced by a factor of two, which indicates a second-order accurate method. The results from the orthogonal seven-point operator (on an orthogonal mesh) show similar behavior.